[Algorithm] Divide and Conquer (2)

이 글은 포스텍 오은진 교수님의 CSED331 알고리즘 수업의 강의 내용과 자료를 기반으로 하고 있습니다.

알고리즘 3주차 첫 번째 강의 노트이다.

Divide and conquer의 좀 더 심화적인 예제들에 대해서 배울 것이다.

참고로 2.Matrix Multiplication 부터는 시험에 안나온다 ㅎㅎ

1. Closest pair of points

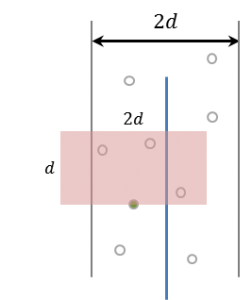
이렇게 점들의 집합이 있을 때, 이 중에서 가장 짧은 거리를 가지는 pair을 구하는 알고리즘을 만들어보자.

정말 간단하게 생각한다면, 그냥 모든 pair을 조사하면 될 것이다.

그러나 이건 $O(n^2)$으로, 좀 느린 편이다.

성능 향상을 위해 divide and conquer을 적용해보자.

• Divide: x median을 구한다

• Conquer: 각 subset에서 closest pair을 구한다

• Combine: 다른 subset까지 고려하여 closest pair을 찾는다

참고: 이 알고리즘은 x축, y축 각각의 기준으로 소팅된 배열을 미리 전달받는다고 가정하고 풉니다. (preprocess)

Divide - Conquer을 거치고 나면 아래와 같은 모습이 될 것이다.

이제 combine을 해야 하는데, 생각해보면 기껏 나눠서 구해놓은 걸 합쳐서 다시 구하면 무슨 의미가 있는건가..?? 싶을 것이다.

바로 이 부분이 알고리즘의 핵심이다. 놀랍게도, combine을 선형시간에 할 수 있다!

아이디어는 제약을 활용하여 추가적으로 계산해야 하는 pair의 경우의 수를 최대한 줄이는 것이다.

왼쪽 subset에서 구한 closest pair의 길이를 $\delta_1$, 오른쪽은 $\delta_2$라고 하자.

우리가 관심있는 것은 $min(\delta_1, \delta_2)=\delta$보다 작은 pair이다.

그렇다면 $\delta$보다 작아질 가능성이 있는 점들만 고려하면 된다.

곧, 이렇게 median line으로부터 좌우로 $\delta$거리 만큼만을 신경쓰면 된다는 것이다.

나중을 위해서 y축으로 정렬도 해놓자.

이제 이 영역을 더 잘게, $\delta/2$ 길이의 정사각형으로 나눠보자.

이렇게 나누면 매우 놀라운 사실을 알아낼 수 있다.

각 정사각형에는 2개 이상의 점이 들어갈 수 없다

왜 그럴까? 간단하다.

만약 2개 이상의 점이 들어간다면, $\delta$보다 작은 pair가 생겨버리고, 이는 모순이기 때문이다.

그럼 이 사실로부터 또 다른 놀라운 사실을 알아낼 수 있다.

2행 이상 차이나는 두 점은 무조건 그 거리차가 $\delta$ 이상이다

이는 우리가 조사해야 하는 점의 숫자를 획기적으로 줄여준다.

한 행에는 4개의 박스가 들어가고, 2행 이상 차이나는 것은 버리면 되므로 11개의 박스(= 11개의 점)만 비교하면 된다!

사실 대부분의 사이트에서는 7개로 설명한다. 이는 박스의 기준점을 어떻게 잡느냐의 차이이다.

¹

이렇게 점을 기준으로 박스를 나누면 7개라고 볼 수 있고,

이렇게 기준점 없이 그냥 나누면 11개라고 볼 수 있는 것이다.

어떻게 풀어도 상관은 없다. 다만 계수가 더 작은 쪽이 좋지 않나 싶다.

여하튼, y축 기준으로 아래에서부터 올라오면서, 각 점에 대해서 최대 11개의 점만 비교해보면 된다는 것이고, 이는 combine이 선형시간에 이뤄진다는 것을 의미한다!

Time complexity

이제 time complexity를 구해보자.

median을 구하고 분할하는데 $O(n)$

sub problem은 $2T(n/2)$

pre-sorting이 되어있으므로 combine 단계에서, 중앙으로부터 $\delta$ 거리 안에 있는 점들을 모으고 이들을 정렬하는데 $O(n)$

따라서 $T(n)\leq 2T(n/2)+O(n)\rightarrow T(n)=O(nlogn)$ 이다!

2. Matrix Multiplication

matrix multiplication은 우리가 배운대로 그냥 하면 $O(n^3)$이 걸린다.

상당히 느리다고 할 수 있다.

사실 딱히 개선점이 보이지도 않는다.

연산들이 전부 독립처럼 보이기 때문이다.

그런데, 놀랍게도 스트라센 이라는 사람이 이걸 줄이는 방법을 찾아냈다.

우선 divide and conquer을 적용해보자

그런데 이렇게 되면, 8개의 sub problem이 생긴다.

곧 $T(n)\leq 8\cdot T(n/2)+O(n^2)=>T(n)=O(n^3)$이므로 달라지는게 없다는 것을 알 수 있다.

스트라센은 이 공통점이 없어보이는 연산을 놀랍게도 7개의 sub problem으로 줄이는 데에 성공했다.

complexity를 계산해보면 약 $O(n^{2.81})$로, 조금 나아졌음을 알 수 있다.

최신 연구 상으로는 1.5 정도까지 떨어졌다고 한다.

3. Polynomial multiplication

다항식의 곱셉을 해보자.

$A(x)=a_0+a_1x+\cdots+a_dx^d$ 와 $B(x)=b_0+b_1x+\cdots+b_dx^d$가 있다.

이 두 다항식의 곱을 $C(x)=A(x)\cdot B(x)=c_0+c_1x+\cdots+c_{2d}x^{2d}$ 이라고 하자.

우리가 일반적으로 하는 것처럼 $C(x)$를 구하려면 얼마나 걸릴까?

우선 $c_k=a_0b_k+a_1b_{k-1}+\cdots+a_kb_0=\sum_{i=0}^{k} a_ib_{k-i}$ 이므로, $c_k$를 구하는데에는 $O(k)$만큼 걸린다.

$0\leq k \leq 2d$이므로, 총 $\sum_{k=0}^{2d} O(k)=O(d^2)$만큼의 시간이 걸린다!

과연 이걸 향상시킬 수 있을까?

놀랍게도, 가능하다! 무려 $O(d logd)$으로 말이다.

1. Another Repres. of polynomials

우리는 현재 다항식을 계수들로 표현하고 있다. ($a_0, a_1 \cdots$)

알고리즘의 핵심은 다항식을 이것과는 다른 방식-distinct points-로 표현하는 것이다.

예를 들면 이런 식이다.

어떻게 이게 가능할까?

이는 아래의 theorem 때문이다.

A degree $d$ polynomial is uniquely characterized by its values at any $d+1$ distinct points

이렇게 distinct points로 표현하는 방법은 기존의 계수 표현법과 자유롭게 전환이 가능하다.

이 전환을 evaluataion, interpolation이라고 한다.

이제 이것을 다항식의 곱셈에 적용해보자.

$C(x)$ 는 $2d+1$개의 distinct points로 표현될 수 있으므로, 각 point $x_i$에 대해 $C(x_i)=A(x_i)B(x_i)$를 구해주면 되는 것이다.

2. Evaluation by divide and conquer

위 알고리즘에서 가장 핵심은 evaluation이다. 유일하게 복잡도를 줄일 수 있는 단계이기 때문이다.

그럼 어떻게 해야 줄일 수 있을까?

Divide and conquer를 적용하기 위해, $A(x)$를 짝수항과 홀수항으로 쪼개보자.

짝수항을 $A_e(x)=a_0+a_2x+a_4x^2+\cdots+a_dx^{d/2}$ 로 묶고

홀수항을 $A_o(x)=a_1+a_3x+a_5x^2+\cdots+a_{d-1}x^{d/2-1}$ 로 묶으면

$A(x)=a_0+a_1x+\cdots+a_dx^d$를 $A_e(x^2)+xA_o(x^2)$ 로 표현할 수 있다.

이제 $n\geq 2d+1$개의 distinct points를 $\pm x_0, \pm x_1, \cdots, \pm x_{n/2-1}$로 잡아보자.

그러면 놀랍게도,

$A(x_i)=A_e(x_i^2)+x_iA_o(x_i^2)$

$A(-x_i)=A_e(x_i^2)-x_iA_o(x_i^2)$

위 두 식은 서로 계산해야 할 것이 겹쳐지게 된다!

이로 인해, $n$개의 point에 대해 계산해야 하는 문제가 $n/2$개의 point에 대해 계산해야 하는 2개의 소문제로 나눠지게 된다.

따라서, $T(n)=2T(n/2)+O(n) \rightarrow O(nlogn)$이 되어 향상된 다항식 곱셈 알고리즘을 얻을 수 있다.

3. Evaluation by FFT

근데 이렇게 해서 재귀가 가능할까?

곰곰히 생각해보자. $n/2$에서 $n/4$로 가려면 $x_0^2, x_1^2, \cdots, x_{n/2-1}^2$를 $\pm$으로 2개씩 묶어야 하는데, 전부 다 양수라서 묶을 수가 없다.

어떻게 해야할까?

제곱해서 음수가 될 수 있는 수, complex number를 도입하면 된다!

그럼 어떤 complex number를 잡아야 할까?

이를 알아보기 위해 과정을 reverse engineer 해보자.

재귀의 끝 $T(1)$에서 $+1$을 point로 잡았다고 해보자.

그럼 $T(2)$에서는 $\sqrt{+1}=\pm 1$이 point일 것이고,

$T(4)$에서는 $\sqrt{1}=\pm 1, \sqrt{-1}=\pm i$가 point일 것이다.

이걸 일반화하면, $T(n)$에서는 $z^n=1$의 complex solution들이 point가 된다는 것을 알 수 있다.

$z^n=1$를 풀기 위해서는 드무아브르의 정리를 알아야 하는데, 기억이 나지 않는 분들은 여기에서 3-1 단위근과 이형방정식을 보면 된다.

결론적으로 $z^n=1$의 해는 $z_k=\cos{\frac{2k\pi}{n}}+i\sin{\frac{2k\pi}{n}}, k=0,1,2,\cdots,n-1$ 이다.

여기에 오일러 정리를 끼얹어서 다시 한번 정리해보자.

$\omega=e^{2\pi i/n}$라고 하면, n개의 해는 각각 $1, \omega, \omega ^2, \cdots, \omega ^{n-1}$이 된다.

이 해들의 기하학적 의미는 단위원에 내접하는 정 n각형의 꼭짓점이라 할 수 있다.

위 그림에서 보다시피, n이 짝수라면 $\omega ^{n/2+j}$와 $\omega ^j$는 서로 $\pm$의 관계를 가짐을 알 수 있다.

곧, $(\omega ^j)^2$를 $T(n/2)$의 point로 잡을 수 있고, 이같은 방식으로 재귀를 하면 된다.

이렇게 허수를 도입해서 푸는 알고리즘을 FFT(fast fourier transform)이라고 한다.

아래는 FFT의 수도코드이다.

4. 출처 및 참고

The Casterian

1. https://casterian.net/archives/92 ↩