[Algorithm] Divide and Conquer (1)

이 글은 포스텍 오은진 교수님의 CSED331 알고리즘 수업의 강의 내용과 자료를 기반으로 하고 있습니다.

CSED331 알고리즘 수업 2주차 강의 내용 요약이다.

이번 주차의 핵심적인 주제는 Divide and Conquer이다.

이 기법을 적용하는 예시들을 하나하나 알아볼 것이다.

참고로 Divide and Conquer을 분석할 때에는 세가지를 생각하면 된다.

• Divide: 문제가 어떻게 나눠지느냐?

• Conquer: 나눠진 문제들을 각각 어떻게 푸느냐?

• [optionally] Combine: 나눠진 문제들을 어떻게 합치느냐

1. Binary Search

Binary Search는 Divide and Conquer의 대표적인 예시이다.

• Divide: 중간값과 비교한다

• Conquer: 재귀적으로 한 sub array를 탐색한다.

• Combine: 필요 x

곧, $T(n)=T(\left \lceil n/2 \right \rceil)+O(1)$ 이 된다.

Master Theorem에 의해, $O(logn)$ 이다.

2. Merge Sort

Merge Sort도 대표적인 예시이다.

• Divide: 중간 지점을 찾는다

• Conquer: 재귀적으로 두 sub array를 정렬한다

• Combine: 두 sub array를 순서대로 합친다

기본적인 아이디어는 큰 array를 작게 나눠서 정렬하고, 다시 합쳐서 전체를 정렬한다는 것이다.

각 단계에서 두 개로 나눠지고, 두 sub array를 합치는 데에는 linear time이 걸리므로

$T(n)=2T(n/2)+O(n)$, 곧 $O(nlogn)$ 이다.

An $nlogn$ lower bound for sorting

Merge Sort는 optimal 할까?

위 질문에 답하기 위해서는 comparision based sorting algorithm을 tree로 생각해보는 것이 필요하다.

이런 식으로 말이다.

이렇게 comparision based sort tree에서의 depth는 root에서 leaf까지 가는 경로 중 가장 긴 것의 길이, 곧 worst-case time complexity로 생각할 수 있다.

이때 leaf는 정렬의 결과이므로, 총 $n!$개가 있다.

Depth d인 Binary tree가 최대 $2^d$의 leaf node를 가진다는 것을 생각해보면, 위 tree의 최소 depth는 $log(n!)$이 된다.

이때 $log(n!)\geq c\cdot nlogn$이므로, $\Omega(nlogn)$이 된다.

이 말은, 그 어떤 comparision based sorting이라도 최악의 경우에 $\Omega(nlogn)$의 비교를 해야한다는 말이므로, merge sort는 optimal하다고 결론 내릴 수 있다.

3. Finding Medians and Selection

이제 좀 더 재밌는 알고리즘으로 들어와보자.

median을 찾으려면 어떻게 해야할까?

위에서 merge sort를 배웠으니, 간단하게 정렬하고 찾으면 될 것 같다.

그런데 이러면 꽤 손해가 크다.

고작 중앙값 하나 찾는다고 모든 원소들을 움직일 필요가 있을까?

아니다. 분명 개선의 여지가 있을 것이다.

자 그러면, 문제를 좀 더 일반화해보자.

median이 아니라, k번째로 작은 원소를 찾는 것이다.

이런 문제를 selection이라고 한다.

SELECTION
Input: A list of numbers S; an integer k
Output: The kth smallest element of S

Selection을 어떻게 divide and conquer로 접근해야 할까?

바로 임의의 수를 기준으로, 총 3개의 그룹으로 나누는 것이다.

나눈 그룹을 재귀적으로 탐색해다가 보면 결국 원하는 수를 찾을 수 있을 것이다.

그러나, 이 방법은 심각하게 고려해야 할 점이 있다.

바로 임의의 수를 어떻게 뽑느냐에 매우 의존한다는 것이다.

예를 들어, 계속해서 제일 작은 수만 뽑는다면 어떻게 될까?

0개, 1개, n-1개의 그룹으로 계속 나뉘게 될테니

$T(n)=T(n-1)+O(n)$, 즉 $O(n^2)$이라는 심각한 복잡도를 가지게 된다.

그럼 어떻게 임의의 수를 뽑아야 할까?

두가지 접근법을 알아보자.

1. Randomized Selection

첫번째로는, 단순하게 랜덤하게 뽑는 것이다.

아까랑 뭐가 달라졌나 싶을 것이다.

그러나 이 접근은 위에서 언급한 최악의 경우는 매우 드물다는 사실 덕분에 생각보다 효율적이다.

미리 결과부터 보자면, 좋은 수가 뽑힌다면 무려 $O(n)$까지 복잡도를 단축시킬 수 있다!

여기서 좋은 수란, 상위 25%~75% 사이에 위치하는 수를 말한다.

그렇다면, 과연 몇 번의 시행을 해야 좋은 수를 뽑을 수 있을까?

이를 위해선 아래의 Lemma를 알아야 한다.

On average a fair coin needs to be tossed two times before a heads is seen

좋은 수가 나올 확률은 $1/2$로, 우리가 구하려는 문제는 lemma의 상황과 완벽히 일치한다.

곧, 좋은 수는 평균 2번의 시행으로 뽑을 수 있다.

Time complexity

이제 그럼 time complexity를 구해보자.

수를 뽑고, 이것이 좋은 수인지 판단하려면 전체와 비교해야 하므로 $O(n)$이 걸린다.

이때 평균적으로 두 번의 시행이 필요하므로 $O(2\cdot n)$이다.

만약 좋은 수를 뽑는다면, sub problem은 최대 $3n/4$ 크기를 갖는다.

따라서, $T(n)\leq T(3n/4)+O(2\cdot n)$이고, 곧 $O(n)$이다.

2. Deterministic Selection

이런 랜덤한 방법이 싫다면, median of medians라는 방법도 있다.

Median of medians란 divide and conquer로 상위 30%~70% 사이의 값을 항상 찾아주는 알고리즘이다.

개인적으로 상당히 신박한 알고리즘이라고 생각한다.

median of medians는 아래의 과정으로 진행된다.

1. 데이터 셋을 5개씩 분할한다.

2. 각각의 group을 정렬해 median을 찾는다.

3. 총 $n/5$개의 medians들 중에서 median을 찾는다.

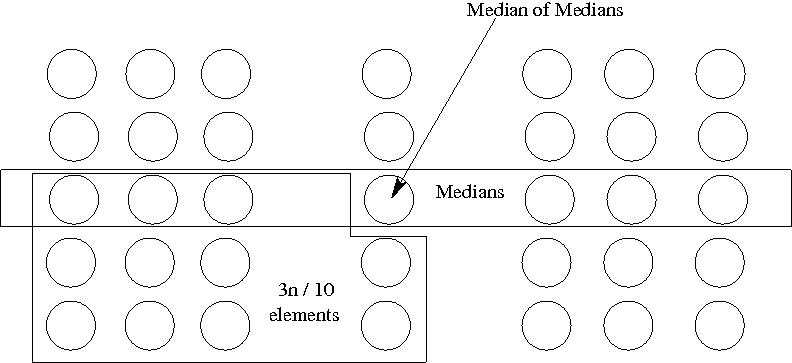
그렇다면 왜 이 알고리즘은 항상 상위 30%~70% 사이의 값을 찾아줄 수 있을까?

마지막 단계에서 찾은 median은 위 사진에서 보다시피 전체를 $3n/10$, $7n/10$으로 분할하기 때문이다.

Time complexity

그럼 전체 time complexity는 어떻게 될까?

각 group을 정렬하는 데에는 상수시간이 걸리므로 $O(1)$.

$n/5$개의 median들 중에서 median을 찾는 것은 $T(n/5)$.

찾은 median으로 전체를 분할하는데에는 선형 시간이 걸리므로 $O(n)$.

이때 분할은 데이터 셋을 최대 $7n/10$으로 분할하므로

$T(n)\leq O(n)+T(n/5)+O(n)+T(7n/10)$이고, 곧 $T(n)=O(n)$이다.

위 식이 왜 O(n)인지는 귀납법으로 증명하는게 편하다.

귀납법 증명

위 링크에 증명이 상세하게 적혀있으니, 참고하면 좋다.