[Algorithm] Introduction (2)
이 글은 포스텍 오은진 교수님의 CSED331 알고리즘 수업의 강의 내용과 자료를 기반으로 하고 있습니다.
알고리즘 두번째 1주차 강의 요약이다.
실상 중요한건 master theorem 밖에 없다 ㅎㅎ
1. Convex Hulls
Convex hull 알고리즘은 2차원 평면 상에 여러개의 점이 있을 때 그 점들 중에서 일부를 이어서, 내부에 모든 점을 포함시키는 polygon을 만드는 알고리즘이다.
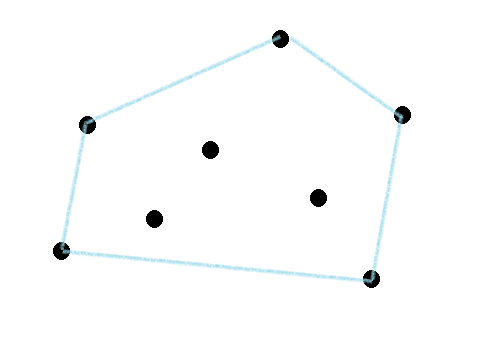
예를 들어 아래와 같은 점들이 있을 때
아래와 같은 polygon을 만드는 것이다.
아이디어가 뭘까?
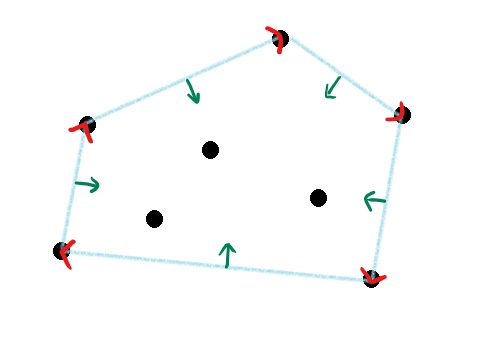
Polygon을 유심히 살펴보면, polygon의 각 edge의 좌측에는 점들이 없다는 것을 알 수 있다.
곧, 좌측에 점이 존재하지 않는 edge들을 구하면 되는 것이다.
그럼 좌측에 점이 있는지 없는지 어떻게 판단할까?
위처럼 $r$이 $\overrightarrow{pq}$의 좌측에 있는지를 보려면
$\overrightarrow{pq}$과 $\overrightarrow{pr}$의 기울기를 비교하면 된다.
무려 상수시간 $O(1)$에 할 수 있다!
여기서 핵심적인 질문.
그래서 좌측에 점이 없는 edge들을 어떻게 찾는데?
당장 떠오르는 건 모든 edge들을 조사한 다음, 좌측에 점이 없는 것만 골라내는 brute force 방식일 것이다.
근데 이렇게 되면 $\binom{n}{2}$개의 edge들을 각각 $n-2$개의 점들과 비교 연산을 해야하므로 무려 $O(n^3)$이라는 괴랄한 time complexity가 나온다.
이걸 어떻게 개선해야 할까?
Graham’s scan
Edge를 고르는게 아니라, 역으로 edge가 될 수 없는 point를 걸러낸다고 생각해보자.
다른 point와 죄다 비교하지 않고, 어떤 point $q$가 edge가 될 수 있는 point인지 아닌지 판단할 수 있는 가장 간단한 방법이 무엇일까?

그림처럼, 전 후로 $p, r$을 뽑고, $q$가 $\overrightarrow{pr}$의 오른쪽에 있는지 왼쪽에 판단하기만 하면 된다.
이러면 point를 걸러내는 데 걸리는 시간이 상수시간으로 대폭 줄어든다.
그렇다면, 맨 왼쪽 point부터 시작해서 하나하나 차근차근 걸러낸다면 선형시간에 convex hull을 찾을 수 있지 않을까?
이것이 Graham’s scan의 메인 아이디어이다.
아마 뭔가 알듯 말듯 한 그런 기분일 것이다.
예시를 보면서 제대로 이해해보자.
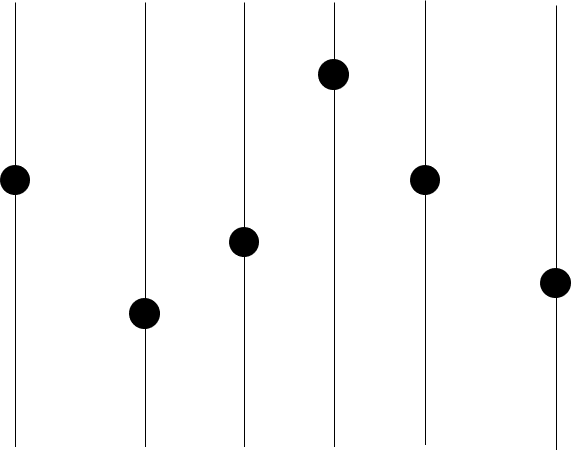
우선 점들을 x축 기준으로 정렬해야 한다.
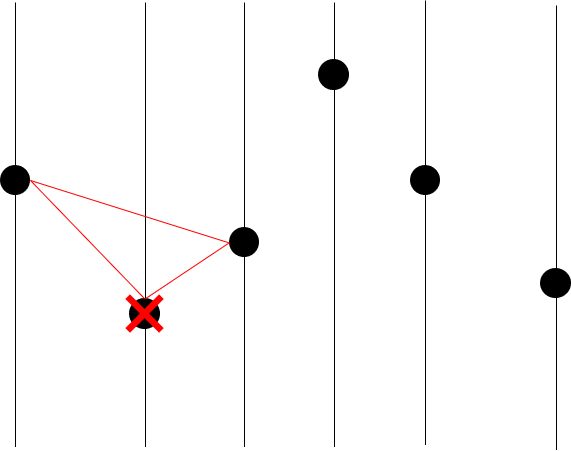
맨 왼쪽 점은 당연히 convex hull vertex이다.
그러면 두 번째 점이 convex hull vertex인지 아닌지 판정해보자.
두 번째 점 기준으로 좌측, 우측 점 하나씩을 뽑고 삼각형을 그려보자.
그러면 두 번째 점이 아래쪽에 있기 때문에 convex hull vertex가 아님을 알 수 있다.
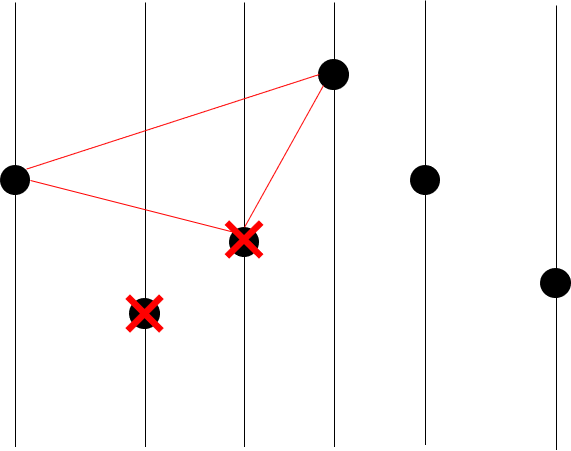
그럼 이제 세 번째 점이 convex hull vertex인지 아닌지 판정해보자.
세 번째 점 기준으로 좌측, 우측 점 하나씩을 뽑자.
두 번째 점은 이미 버려졌기 때문에, 첫 번째 점과 네 번째 점을 뽑으면 된다.
역시 삼각형을 그려보면 아래쪽에 있기 때문에, 세 번째 점도 버리면 된다.
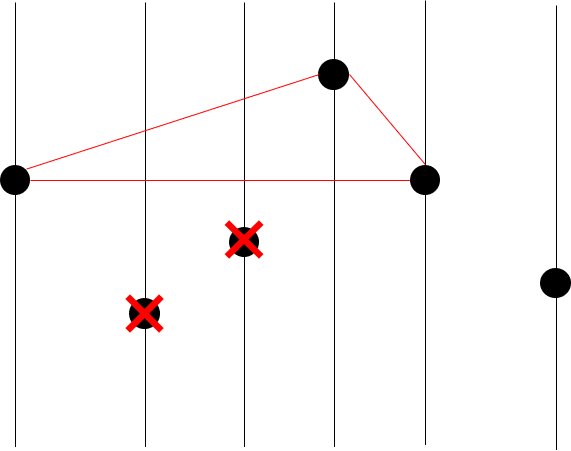
이제 네 번째 점이 convex hull vertex인지 아닌지 판정해보자.
좌측 점으로 첫 번째 점, 우측 점으로 다섯 번째 점을 뽑는다.
삼각형을 그려보면 위쪽에 있기 때문에 네 번째 점은 버리지 않는다.
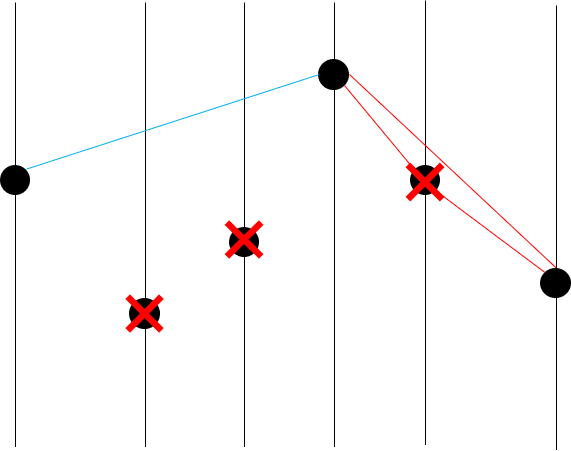
이제 다섯 번째 점이 convex hull vertex인지 아닌지 판정해보자.
앞선 과정에서 네 번째 점이 버려지지 않았기 때문에, 좌측 점으로 네 번째 점, 우측 점으로 여섯 번째 점을 뽑는다.
삼각형을 그려보면 아래쪽에 있기 때문에 다섯 번째 점은 버려진다.
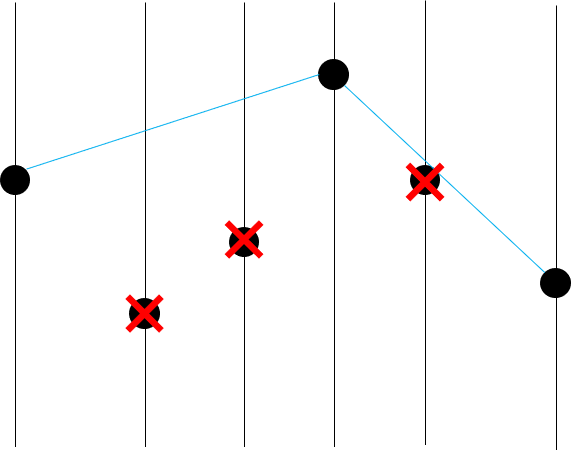
그러면 이제 convex hull의 위쪽 반은 구해졌다!
아래쪽 반을 구하기 위해서는 위의 과정을 우측 점부터 다시 하면 된다.
이제 Graham’s scan의 메인 아이디어가 어떤 것인지 이해했을 것이다!
그럼 이제 Graham’s scand을 맞이하러 가자.
Algorithm
우선 x축으로 point들을 정렬하자.
이 정렬된 point의 list를 $L$이라고 하자.
이제 아래의 3단계를 convex hull이 구해질 때까지 반복하면 된다!
(0) pick $p,q,r$ from $L$ in order.
(1) If $r$ lies to the right of $\overrightarrow{pq}$, we move one step forward in L.
(2) Otherwise, remove $q$ from the sorted list and move one step backward in L if possible.
우리가 위에서 했던 과정과 하나도 다를 것이 없다.
다만 주의할 점은 $p$를 어떻게 잡느냐이다.
만약 $q$를 버리지 않았으면 $p$를 앞으로 한칸 옮기고, 실패했다면 $p$를 뒤로 한칸 옮겨야 한다. (물론 $p$가 맨 왼쪽이라면 더 뒤로 가진 않는다)
PPT를 보면서 과정을 따라해보면 이 말이 무슨 말인지 금방 이해할 수 있을 것이다.
Time complexity
이제 Time complexity를 구해보자.
우선 정렬하는 데에는 $O(nlogn)$이 걸린다.
전체 loop에서 (1) 과정을 몇 번 들어갈까?
다른 말로, $r$이 몇 번 전진할까?
간단하다. 맨 처음 뽑은 $p,q$ 점을 제외한 모든 점을 $r$은 한 번씩 방문한다.
따라서 (1) 과정은 $n-2$번 들어간다
그러면 (2) 과정은?
다른 말로, 몇 번이나 $q$를 버릴까?
간단하다. 결과적으로 convex hull vertex가 아닌 점은 모두 버리기 때문에 총 $n-h$번 버린다. ($h$는 vertices of convex hull)
따라서 (2) 과정은 $n-h$번 들어간다.
그럼 loop는 선형시간이 걸리므로, $O(nlogn)+O(n)=O(nlogn)$이 걸린다!
$O(n^3)$에 비하면 정말 선녀같아 졌다.
2. Little taste of divide and conquer
다음시간부터 본격적으로 divide and conquer를 다룰 것이다.
이번 시간에는 살짝 혀만 담궜다 빼보자.
1. Multiplication
n-bit 곱셈을 해보자.
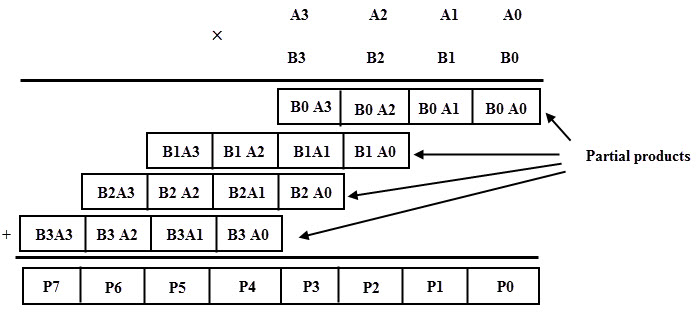
디시설 때 배웠겠지만, 위와 같이 하면 된다.
그럼 이걸 divide and conquer로 풀어보자.
$n/2$로 쪼갠다면 위와 같이 전개할 수 있을 것이다.
이렇게 되면 $n/2$짜리 문제가 4개가 생성되는데, 혹시 이걸 더 줄일 수 있을까?
놀랍게도 가능하다.
위 처럼 $x_L y_R + x_R y_L$을 쪼개면 $x_L y_L,\;x_R y_R,\;(x_L + x_R)(y_L + y_R)$ 이렇게 문제가 3개로 줄어든다
그럼 이 알고리즘의 time complexity를 점화식으로 써보면 $T(n)=3\cdot T(n/2)+O(n)$인데, 이걸 어떻게 풀어야 할까?
2. Recurrence relations
점화식을 시각적으로 표현해보면 위와 같다.
그럼 $k-th\;level$에서의 complexity는 $O(n/2^k)\cdot 3^k$일 것이고, 이걸 전부 합하면
이 된다.
따라서 우리가 구하고자 하는 점화식의 해는 $O(n^{log_2{3}})$이 됨을 알 수 있다.
3. Master Theorem
근데 그러면 이걸 일반화 시킬 수 있을까?
그러니까, $T(n)=a\cdot T(\left \lceil n/b \right \rceil)+O(n^d)$의 해는 무엇일까?
우리가 $T(n)=3\cdot T(n/2)+O(n)$를 구한 아이디어와 동일하게 접근해보자.
그럼 $k-th\;level$에서의 complexity는 $a^k\cdot O((n/b^k)^d)$가 됨을 곰곰히 생각해보면 알 수 있다.
그리고 이 식을 요리조리 정리해보면 $O(n^d)\cdot (a/b^d)^k$가 되는데, 이걸 전부 합해보자.
고등학교 수학이 기억난다면, 이 식은 $a/b^d$에 따라서 값이 달라진다는 것을 알 수 있을 것이다.
-
만약 $a/b^d<1$이라면?
감소 수열이므로 $O(n^d)$
-
만약 $a/b^d=1$이라면?
시그마 위의 값이 곱해져서 $O(n^dlog_b{n})$
-
만약 $a/b^d>1$이라면?
증가 수열이므로 $S_n=\frac{a(1-r^{n+1})}{1-r}$에서 $O(a\cdot r^n)$임을 알 수 있다.
구해보면
$\therefore O(n^{log_b{a}})$
정리하자면 아래와 같다.
이렇게 divide and conquer에서 나올 수 있는 점화식에 대한 공식이 master theorem이다.
한 번 의미를 해석해보자.
$a/b^d$에서 $a$와 $b^d$는 각각 뭘 의미할까? 곰곰히 생각해보면 아래와 같음을 알 수 있다.
- $a$: rate of sub problem proliferation (RSP)
- $b^d$: rate of work shirinkage (RWS)
이를 통해 master theorem을 해석해보면
sub problem이 늘어나는 것 보다 work가 줄어드는게 빠르면 ($a/b^d < 1$) $O(n^d)$
sub problem이 늘어나는 것과 work가 줄어드는 것이 같으면 ($a/b^d = 1$) $O(n^d logn)$
sub problem이 늘어나는 것 보다 work가 늘어나는게 빠르면 ($a/b^d > 1$) $O(n^{log_b{a}})$
이런 식으로 생각하면 좀 더 외우기 편하다!