[Algorithm] Introduction (1)

이 글은 포스텍 오은진 교수님의 CSED331 알고리즘 수업의 강의 내용과 자료를 기반으로 하고 있습니다.

CSED331 알고리즘 수업 1주차 강의 내용 요약이다.

1. 알고리즘이란 무엇인가?

PPT 의 내용 상으론 알고리즘이란 A step-by-step procedure to solve a problem 이라고 한다.

알고리즘의 특징은 언어 비 종속적이라는 것이다.

우리가 어떤 로직을 짤 때에 흔히 어떤 언어를 쓰느냐에 따라 로직이 많이 달라지곤 하는데, 알고리즘은 그럴 필요가 없다.

그래서 알고리즘을 표현할 때에는 특정 언어가 아니라 수도코드(pseudo-code) 또는 영어로 그냥 표현한다.

2. 알고리즘의 효율성

언어에 비 종속적이라는 말은, 우리가 흔히 프로그램 성능 테스트 하듯이 시간 체크를 할 수 없다는 것이다.

그래서 알고리즘을 평가할 때에는 basic operation($+ , - , * , / , $comparision) 을 unit time 이 걸린다고 가정하고 평가한다.

평가 지표는 어떤 input이 들어왔을 때 얼마나 연산이 수행되는지이다.

보통 input 의 사이즈를 $n$ 으로 두고, $n$ 에 대한 함수로써 이를 표시한다.

예를 들면 $n, n^2, n^3, 1.5^n, 2^n, n!$ 등이 있겠다.

그렇다면 여기서 한가지 물음이 생긴다.

이 n 에 대한 함수들을 어떻게 비교해야 하는가?

그래서 나온게 asymptotic notation 이다.

이것에는 총 4가지 종류가 있다.

• Big $O$
• Little $o$
• Big $\Omega$
• Little $\omega$

각각이 의미하는 바는 아래의 표와 같다

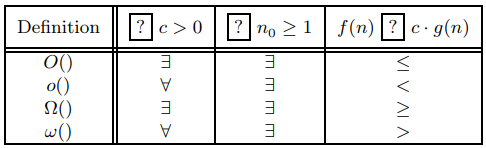
한 가지 주의해서 해석해야 할 점은, 제약 조건을 앞에서부터 읽어야 한다.

그러니까 $\forall c \; \exists n_0 \; P(x,y)$ 와 $\exists c \; \forall n_0 \; P(x,y)$ 은 다르다.

전자는 모든 $c$ 에 대해서 P(x,y)가 참이 되는 어떠한 $n_0$가 존재할 때 참이다.

후자는 모든 $n_0$에 대해서 P(x,y)가 참이 될 수 있는 $c$ 가 존재할 때 참이다.

지난 학기에 전산수학 배울 때 처음에는 이게 뭔 소린가 싶었지만 곰곰히 생각해보니 당연한 말이었다.

그리고 몇 가지 Properties 가 있다.

• 상수 곱은 무시될 수 있다.
• $a>b$ 일때 $n^a$ 는 $n^b$ 를 이긴다.
• 지수 함수는 다항식을 이긴다 (ex: $3^n$ dominates $n^5$)
• 다항식은 로그함수를 이긴다. (ex : $n$ dominates $log^3n$)

이런 commonsense rules 을 잘 알아둬야 문제를 풀 때 좀 쉽게 풀 수 있다.

그런데 개인적으로는 그냥 알아두기 보다는 왜 그런지 한번쯤은 증명해보는 걸 추천한다.