[AI] Reinforcement Learning (1)

이 글은 포스텍 이근배 교수님의 CSED442 인공지능 수업의 강의 내용과 자료를 기반으로 하고 있습니다.

이번 포스트에서는 요즘 핫한 강화학습을 다룬다.

개인적으로 꽤 흥미로웠던 주제이기도 했다.

아마 MDP를 잘 이해했다면 전혀 어렵지 않을 것이다.

참고로 다음 수업인 probability 파트는 너무 확통 기초 of 기초라서 딱히 정리할 가치를 못느껴 따로 포스팅 하지 않을 예정이다.

아마 전산수학, 확통, 공기통 중 하나라도 중간고사 범위 전까지 들었으면 매우 쉽게 이해할 수 있을 것이다.

1. Reinforcement Learning

Reinforcement Learning, 즉 강화학습이란 action에 대한 feedback을 받고 전략을 수정시켜나가는 행동 방법을 말한다.

이때 feedback은 reward의 형태로 들어오게 되고, 이는 전략을 수정해나가는 방향이 expected reward를 최대화하는 방향임을 시사한다.

감이 좋은 사람이라면 우리가 하고자 하는 것이 MDP와 별반 다를 것 없다는 것을 알아챘을 것이다.

다만 아주 큰 차이점이 생긴다.

바로 $T, R$을 모른다는 점이다.

다시말해 agent는 state와 action이 존재한다는 것만 알지, 어느정도의 확률로 state에 도착할지도, 해당 state로 이동하면 어떤 reward를 받는지도 전혀 모른다.

무작정 부딪혀서 배워야만 하는 것이다.

이렇게 부딪히면서 배우는 방식을 Online Learning이라고 한다.

반대로 이전에 배웠던 MDP는 이미 모든 정보를 알고 있으므로, 각 state에서 탐색을 통해 해를 찾아낼 수 있고 이같은 방식을 Offline Solution이라고 한다.

Online과 Offline이 주는 뉘앙스의 차이를 잘 캐치하길 바란다.

2. Model-Based Learning

그럼 무작정 부딪히면서 뭘 배워야 할까?

다시말해 뭘 배워야 policy를 구해낼 수 있을까?

$T, R$을 모르니까 이걸 배우면 될까?

물론 그렇지만, 잘 생각해보면 굳이 그러지 않고 곧바로 $V, Q$를 배워도 policy를 구할 수 있다는 것을 알 수 있다.

전자의 경우를 Model-Based Learning, 후자의 경우를 Model-Free Learning이라고 한다.

우선 Model-Based Learning이란 $T, R$을 배워서 environment에 대한 model을 세우고, 이로부터 value iteration 등을 통해 policy를 구해내는 방법이다.

예를 들어 좌측의 문제가 주어졌다고 하자.

Model-Based Learning은 우선 학습을 위해 몇가지의 episode(sample)을 뽑아낸다. 위 예제에는 4개를 뽑아냈다.

그리고 이로부터 $T,R$에 대한 모델링을 한다.

모델링의 결과가 왜 저렇게 나왔는지는 아마 금방 이해할 것이다.

3. Model-Free Learning

한편 Model-Free Learning은 $V, Q$를 직접적으로 배우는 방식이다.

예를 들어 나이의 기댓값을 구하고자 할 때, model based는 probablity에 대한 모델을 세우고 이로부터 기댓값을 구해내는 반면, model free는 직접적으로 기댓값을 배운다.

개인적으로 그닥 좋은 예제는 아니라고 생각하지만, 전달하고자 하는 바가 어떤 의미인지는 이해했을 것이라 생각한다.

한편 Model-Free Learning에는 두 가지 방식이 있다.

• Passive Reinforcement Learning
• Active Reinforcement Learning

둘의 차이는 간단히 말하자면 $V$를 배우느냐, $Q$를 배우느냐 다.

하나하나 자세히 알아보자.

1. Passive Reinforcement Learning

Passive Reinforcement Learning의 핵심은 state value $V$를 배우는 것이다.

방법은 간단하다. 주어진 fixed policy에 대해 policy evaluation을 하는 것이다.

지난 시간의 내용을 잘 기억하고 있다면 한 가지 의문이 떠올라야 한다.

$T, R$을 모르는데 어떻게 policy evaluation을 하지?

맞다. $T,R$을 모르는 이상 우리가 이전에 하던 방식대로 evaluation을 할 수는 없다.

따라서 우리는 episode, 내지는 sample로부터 evaluation을 하는 방법을 알아야 한다.

Direct Evaluation

가장 간단한 방법은 Direct Evaluation이다.

주어진 policy대로 행동해서 episode들을 만들어내고, 이 episode들을 평균내서 value를 구하는 방법이다.

예를 들어 이렇게 4개의 episode를 뽑아냈다고 하자.

B의 경우 1에서 $-1-1+10=8$, 2에서 $-1-1+10=8$ 이므로 평균 8이다.

E의 경우 1에서 $-1-1+10=8$, 2에서 $-1-1-10=-12$이므로 평균 -2이다.

나머지도 이와같이 구할 수 있다.

근데 이 방식은 단순한 만큼 문제가 참 많다.

문제의 핵심은 모든 state를 개별적으로 learning 한다는 것이다.

이러면 당연히 속도도 느려지고, 결과의 신뢰성도 상당히 떨어지게 된다.

예시만 봐도 바로 알 수 있는데, B와 E가 똑같이 C로 가는데 극단적으로 다른 value를 가지는 건 좀 이해하기 어렵다.

Sample-Based Policy Evaluation

이를 개선하기 위해 bellman equation이 다시 등장한다.

우리가 이걸 직접적으로 사용하지 못하는 이유는 $T,R$을 모르기 때문이다.

그래서 간접적으로 sample을 통해 구하는 아이디어가 sample-based policy evaluation이다.

sample들은 행동을 통해 얻어지는 값이지, 어떤 함수를 통해 계산되는 값이 아님에 주의하자.

감이 안 잡힐수도 있는데, 본질은 이전에 나이의 기댓값을 구하는 예제와 별 다를 것 없다.

근데 sample들을 보면 $k$ 단계 sample을 계속해서 얻어내고 있는데, 이게 가능할까?

단언컨대, 불가능하다. 우리가 Online learning을 하고 있음을 까먹지 말자.

$k$ 단계에서 sample를 한 번 구했으면 거기서 끝이지, 타임머신 타고 $k$단계로 되돌아와서 다시 sample를 구할 순 없다는 말이다.

Temporal Difference Learning

따라서 우리는 각 단계의 single sample로부터만 learning을 해야하고, 이 기법을 Temporal Difference Learning이라고 한다.

다만 단순히 더하면 너무 baias 될 가능성이 높으므로, $\alpha$(learning rate)를 곱해 weighted sum을 한다.

이때 $\alpha$는 약 0.1 정도라고 한다.

PPT에는 없지만 이해를 위해 데모를 하나 들고왔다.

$\alpha=0.5$

지난 시간에 봤던 grid world를 한번 learning 해보자.

화살표 방향은 신경쓰지 말고, learning 하는 것에만 집중하면 된다.

첫 번째 탐색에서 agent가 exit state에 도달했다.

Exit를 하게 되면 +1을 받는다.

그렇게 되면 exit state의 value는 어떻게 될까?

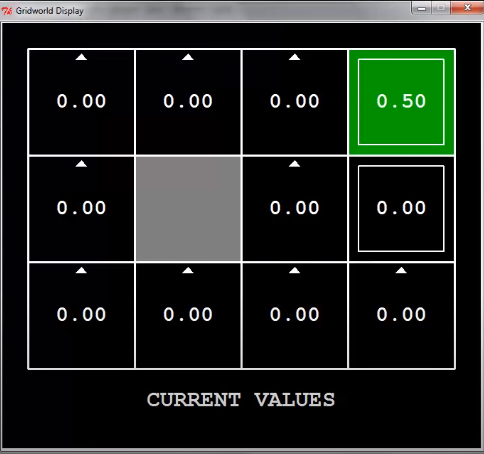
$V^0(s)=0$이므로, $V^1(s)=\alpha \cdot 1=0.5$가 된다.

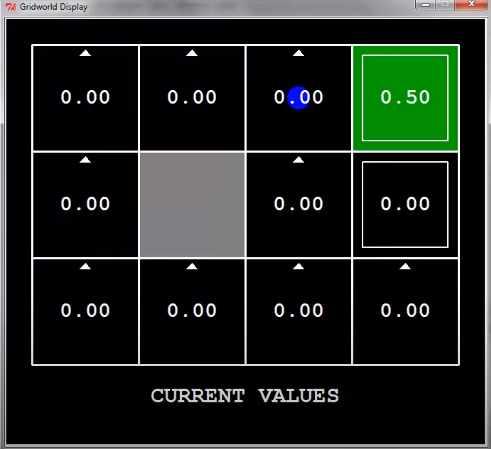
두 번째 탐색에서 agent가 exit state의 바로 전 state에 도착했다.

다음 step에선 이 state의 value는 어떻게 될까?

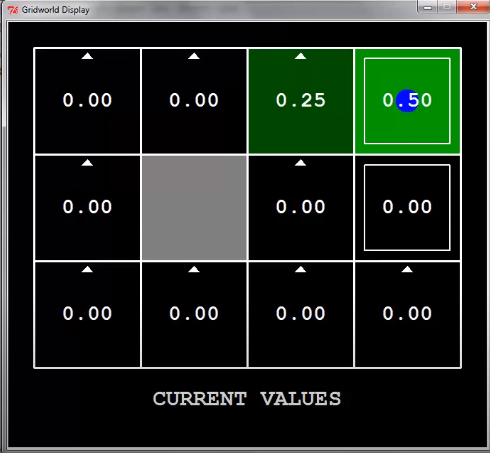
$V^1(s)=0$이므로, $V^2(s)=\alpha \cdot 0.5=0.25$가 된다.

한 번 더 탐색 하면 어떻게 될까?

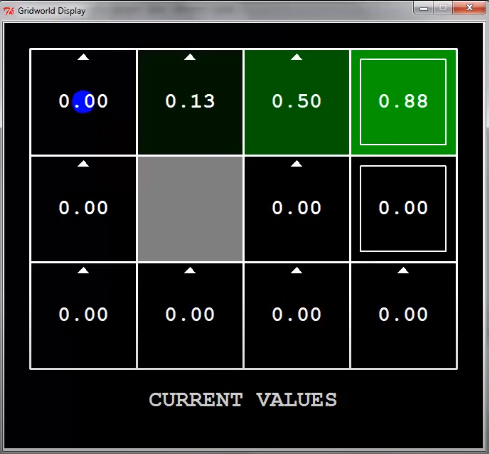
이런 식으로 될 것이다.

이제 대충 감이 오는가?

별 거 없다. 그냥 샘플을 차곡차곡 더할 뿐이다.

2. Active Reinforcement Learning

자 value를 열심히 배웠고, 그럼 새로운 policy는 어떻게 구할 수 있을까?

황당하게도 TD value learning으로는 불가능하다고 한다.

그럼 뭐가 필요할까?

지난 시간에 policy extraction을 배우면서 강조했지만, q-value가 필요하다.

사실 이게 굳이 Q라는 이름을 붙여가면서 강조했던 이유다. 강화학습은 q-value가 없으면 아무것도 못한다.

여하튼, 이렇게 q-value를 배워서 policy를 만들어내는 learning을 active reinforcement learning이라고 한다.

passive와 다른 점은 active는 q-value를 배워야 하기 때문에 어떤 고정된 policy를 따라가는 것이 아니라 agent가 action을 선택해서 배워야 한다.

이 때문에 exploration, exploitation이라는 재밌는 문제가 하나 발생하는데, 나중에 알아보도록 하자.

Q-Learning

우선 q-value의 iterative한 정의는 위와 같다.

$V_K$가 $max Q_k$로 바뀌었다는 것만 기억하면 된다.

Temporal difference learning이랑 별 차이 점이 없다. 그냥 $V$를 $Q$로 바꾼 것이다.

이것도 이해를 위해 데모를 하나 갖고왔다.

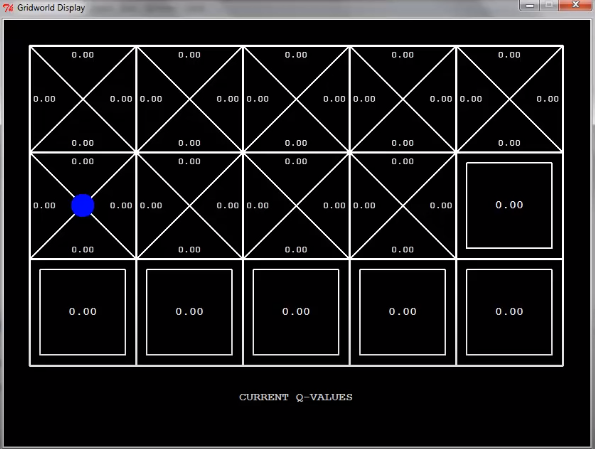
$\alpha=0.5$

조금 확장된 grid world를 q-learning을 해보자.

이때 움직이는 방향은 신경을 쓰지 말자. 그냥 agent가 이렇게 움직이니까 저렇게 배워지는구나 정도만 알면 된다.

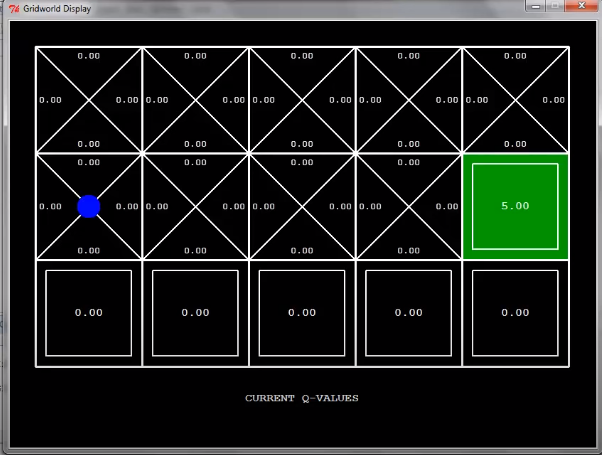
한 번 탐색을 하고 나면 이렇게 될 것이다.

한 번 더 탐색을 하면 exit state의 이전 state의 q-value는 어떻게 될까?

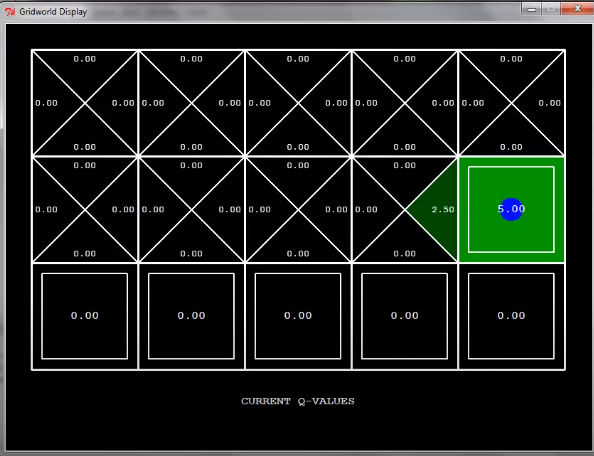
위와 같이 exit state로 움직이는 방향에 대한 q-value가 2.5로 정해지게 된다.

두 번 더 탐색을 하게 되면 어떻게 될까?

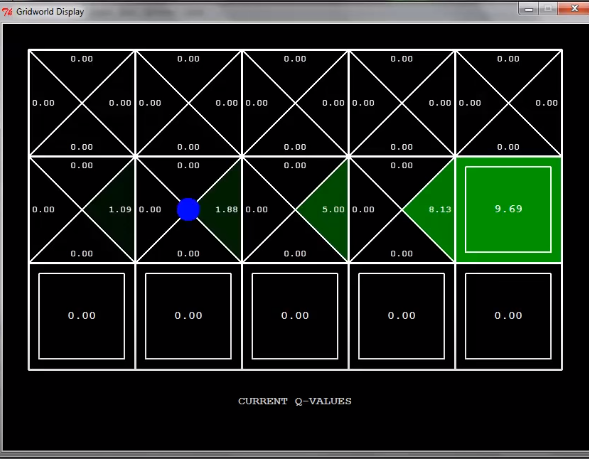
이렇게 누적이 되면서 위와 같이 q-value가 매겨진다.

그럼 만약 아래로 내려가게 되면?

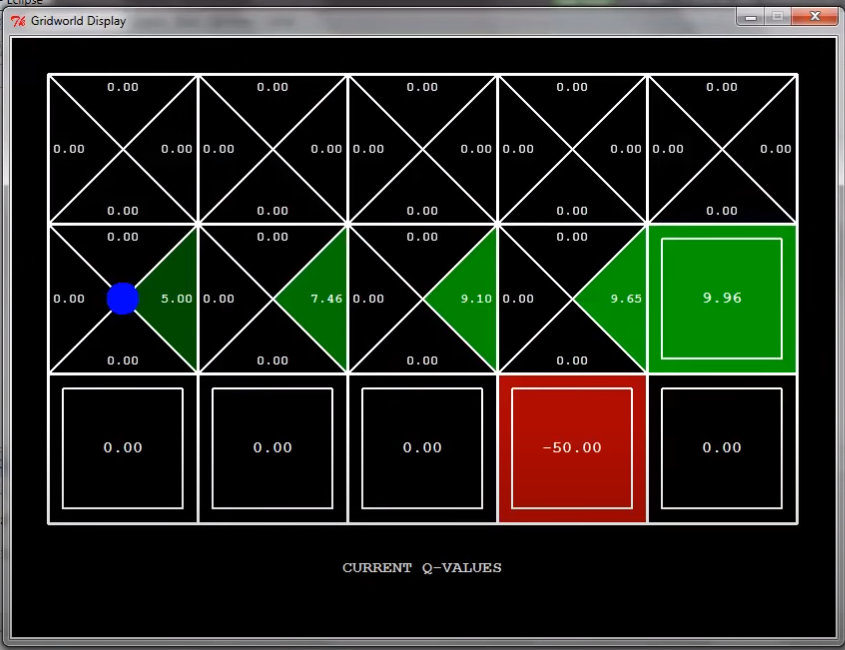
함정에 빠지게 되면 -100을 받으므로, 해당 state는 -50이라는 값을 배우게 된다.

다음 탐색에서 이 state로 다시 가게 되면 그 이전 state의 q-value는 어떻게 될까?

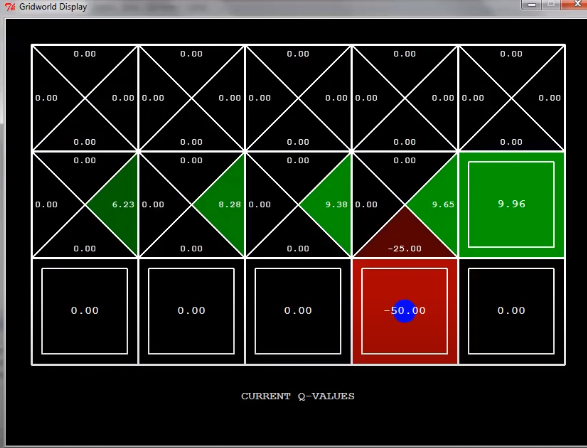
당연히 위와 같이 된다.

이정도면 q-learning이 뭔지 거의 이해했을 것이라고 생각한다.

아래는 데모의 움짤 버전이다.

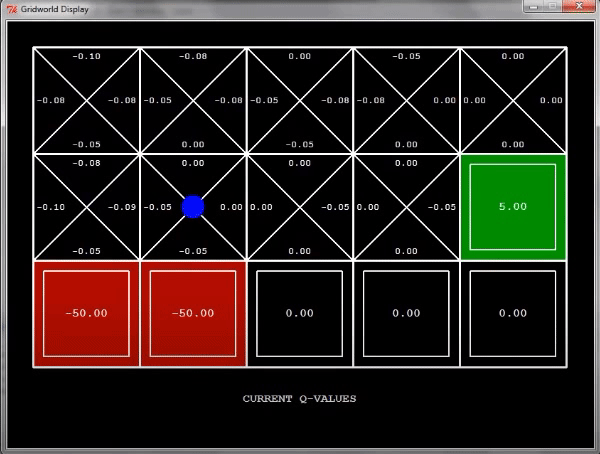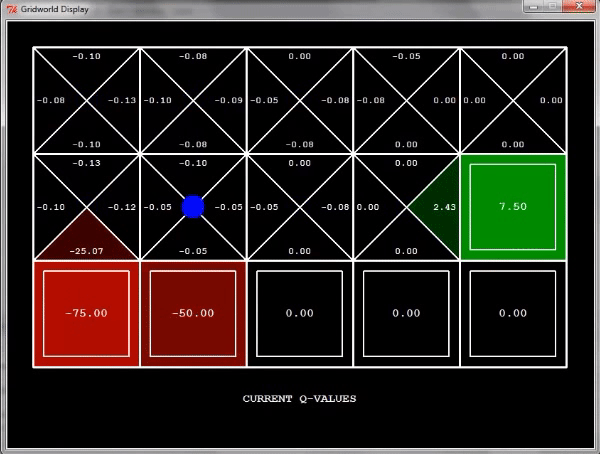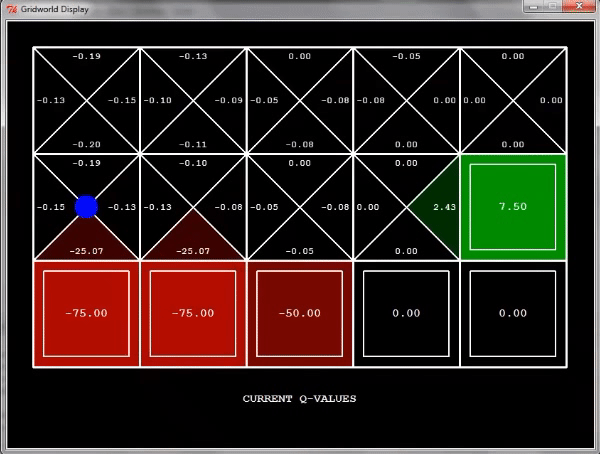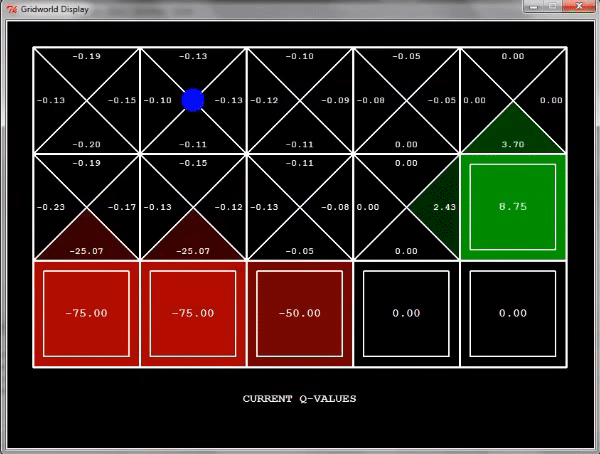
4. Exploration

Q-Learning에 대해서 열심히 배워봤는데, 아마 한 가지 의문이 들 것이다.

어떻게 갈 방향을 결정하지?

이에 관한 문제가 exploration vs exploitation이다.

exploration은 갔던 곳을 또 가는 걸 말하고,

exploitation은 가보지 않았던 곳을 가보는 것을 말한다.

좋은 learning을 위해서라면 이 둘의 비율을 적절히 맞추어야 한다.

가장 간단한 접근법은 그냥 확률에 의존해서 선택하는 것($\epsilon$-greedy)이다.

이를 따르는 agent는 $\epsilon$의 확률로는 랜덤하게 방향을 선택하고 $1-\epsilon$만큼은 현재 정해진 policy를 따른다.

간단하지만, 이미 탐색을 다 한 후에도 계속해서 랜덤하게 움직인다는 단점이 있다.

이를 개선하기 위해 나온 아이디어가 $\epsilon$을 조금씩 줄이는 것이다.

줄이는 방법이란, 가중치 함수 exploration function을 활용하는 것이다.

이는 action a에 의해 방문할 노드에 대해 방문을 안한 만큼 가중치를 줘서 해당 노드로의 방문을 유도하는 식이다.

원래 다음 페이지에 regret이 있는데, 별 중요한 내용도 아니고 그냥 읽어보면 이해가 가는 정도라 생략했다.

5. Approximate Q-Learning

우리가 위에서 배운 q-learning은 모든 q-value table을 저장하고 있어야 가능하다.

근데 이게 실제로 가능할까? 그 작은 팩맨만 해도 state수가 $2^{30}$를 넘어가는데.

당연히 불가능하다.

게다가 state간의 유사도를 활용하지 못한다는 단점도 있다.

아래 예시가 이를 잘 보여준다

Feature-Based Representation

이를 해결하기 위해 나온 표현법이 Feature-Based Representation이다.

말 그대로 state를 어떤 feature들로 표현하겠다는 의미이다.

예를 들어 이 팩맨 게임의 feauture는 goast와의 거리, 가장 가까운 dot, goast 숫자.. 등이 있다.

그럼 이 feature들을 가지고 어떻게 state를 표시할까?

뭐 간단하다. weight sum으로 표현하면 된다.

이전에 adversarial search에서 배운 evaluation function과 비슷한 개념이다.

그럼 이걸 가지고 어떻게 q-learning을 할까?

$Q$를 직접적으로 수정하는게 아니라, weight들을 조절하면 된다.

이걸 Approximate Q-Learning이라고 한다.

이게 왜 가능한지는 조금 있다 배우고, 우선 이걸 제대로 이해하기 위한 예제부터 풀어보자.

만약 이 상황이라면, 어떻게 각각의 weight가 변하게 될까?

아래에 답이 있긴 한데, 한 번 보지 말고 풀어보자. ($\alpha$가 없으므로 $\alpha$를 포함한 식까지만 적어보자.)

답의 의미를 간단하게 해석해보자.

Difference가 음수이므로 $Q$ value를 낮춰야 한다.

그런데 $Q$ value를 직접적으로 낮추지는 않고, $w$를 통해 낮추려고 한다.

이 때 $f_{GST}$가 더 큰 영향을 미치고 있으므로 $(0.5 < 10)$ $w_{GST}$가 더 큰 폭으로 감소한 것이다.

그래서 결과적으로 ghost를 더 싫어하게 됐다!

Leat Squares

자 이제 approximate Q-Learning을 유도해볼 차례이다.

아마 선형대수학을 배웠던 사람이라면 weight sum이 이런 선형근사를 의미한다는 것을 알 것이다.

선형근사의 목표는 error를 최대한 줄이는 것이다.

이 error의 식은 다음과 같다.

이걸 조절하기 위해 우리가 건들 수 있는 유일한 수치는 weight이다.

Weight를 어떻게 조절해야 error를 줄일 수 있을까?

간단한 미적분 문제다.

Error를 weight $w_m$에 대해 편미분 한 값은, error가 $w_m$에 대해 증가하는 비율을 의미한다.

따라서 이것의 반대 방향으로 $w_m$을 이동시켜주면 error가 감소할 것이다. (예시: $y=2x$에서 $x$를 $-2$만큼 이동시키면 $y$가 감소한다!)

이런 과정에 의해 approximate Q-Learning이 유도된 것이다.

6. Policy Search

Approximate Q-Learning이 실제로 사용되기에는 한 가지 문제점이 있다.

비록 feature-based representation이 비슷한 state를 잘 표현 한다지만, 이를 이용해서 얻어지는 V / Q value는 꽤 다를 가능성이 높다.

다시 말해, feature-based representation은 V / Q value를 근사하는데에는 최적의 선택이 아니라는 의미이다.

이를 해결하기 위해 나온 방법이 policy search이다.

Policy search는 우선 이미 주어진 V / Q value가 있는 상태에서, feature-based representation을 통해 weight를 조절해나가면서 더 좋은 policy를 찾는 방법이다.

이전에 배웠던 iterative improvement(local search) - hill climbing을 이용하는 것이다.