[AI] Markov Decision Process (1)

이 글은 포스텍 이근배 교수님의 CSED442 인공지능 수업의 강의 내용과 자료를 기반으로 하고 있습니다.

인공지능 5주차 강의 요약이다.

공부는 예전에 다 해놨는데… 글을 쓰는게 참 시간이 많이 들다보니 투고가 점점 늦어지고 있다.

중간고사 치고 나서는 초안을 그때그때 작성해놓는 습관을 들여봐야겠다.

1. Markov Decision Process

a sequential decision problem for a fully observable, stochastic environment with a Markovian transition model and additive rewards is called a Markov decision process.

정의를 읽다보면 너무 새로운 개념들이 많아서 이게 뭔가.. 싶을 것이다.

예시를 보면서 차근차근 이해해보자.

예를 들어 미로 탐색 인공지능을 구현한다고 해보자.

우리가 이제껏 봐온 agent들은 모두 deterministic하게 움직였다.

다시 말해, 정해준 방향으로만 움직이지 다른 곳으론 움직이지 않았다.

그런데 생각해보면 이건 꽤나 이상적이다.

가끔씩은 의도치 않은 방향으로 가주는 것이 좀 더 현실적인 케이스라 할 수 있겠다.

이와 같이 말이다.

이렇게 확률적으로 움직이는 상황을 stochastic environment라고 한다.

자 그럼, 미로에서 길을 결정할 때 우리는 우리가 이제까지 지나온 길을 생각해야 할까?

물론 그럴수도 있겠지만, 대부분의 경우에는 그걸 기억할 필요는 없다. 헤쳐나가기만 하면 되니까.

이런 식으로 이전의 상태에 대해서는 신경쓰지 않고, 오로지 현재의 상태에만 기반해서 행동을 하는 것을 Markovian transition model이라고 한다.

그럼 이 미로 탐색의 goal은 무엇일까?

미로에서 나가는 것..? 이런 단순한 것에서 벗어나 좀 더 목표를 발전시켜보자.

예를 들어 미로에서 늦게 나가는 것 보다 빨리 나가는 게 좋을테니 최대한 빨리 나가야 한다 등.

이렇게 단순히 어떤 state에 도달하는게 아니라, 좀 더 복합적인 요소를 고려하기 위해 도입한 것이 additive rewards이다.

Reward란 agent가 특정 상태에 도달하거나, 혹은 이동할 때마다 받는 값(living reward)을 말한다.

Agent는 이 reward의 총합이 최대가 되도록 움직인다.

특정 상태에 도달해서 받는 reward란, 예를 들어 출구에 도착하면 +1 reward를 받고, 함정에 빠지면 -1 reward를 받는걸 말한다.

Living reward는 상당히 중요하고, 또 재밌는 개념이다.

예를 들어 미로가 너무 힘들어서 한칸 이동할때마다 일정량의 데미지를 받는다고 해보자.

그러면 agent는 최대한 적게 이동해서 나가려고 할 것이다.

반대로 미로가 너무 좋아서 한칸 이동할 때마다 일정량의 보상을 받는다고 하자.

그러면 agent는 탈출하지 않고 미로를 무한히 돌 것이다.

이 living reward와 관련된 굉장히 재밌는 observation이 있다.

만약 living reward를 극단적인 음수로 만들어버리면 어떻게 될까?

Agent는 탈출이고 뭐고 일단 빨리 이 지옥에서 벗어나고 싶어 자살을 해버린다.

빨간 동그라미를 쳐놓은 state를 보면, 분명 우측으로 가면 죽음에도 불구하고 뛰어들고 있음을 볼 수 있다.

이렇듯, reward를 어떻게 설정하느냐에 따라 agent의 행동 방향이 크게 달라지게 된다.

이 내용들을 종합해서 다시 markov decision process에 대해 정의를 내려보면 다음과 같다.

2. Policy

자 그럼 MDP의 solution는 무엇일까?

확률적으로 움직이기 때문에 이전처럼 sequence of action을 쓸 수는 없다.

대신 각 state에서 어떤 action을 취해야 하는지를 지정해줘야 한다.

이런 전략을 policy라고 한다.

다시 말해, MDP는 optimal policy $\pi^{*}: S \rightarrow A$를 찾는 것이 목표라 할 수 있다.

이때 optimal policy란 expected utility(calculated reward)를 최대화 하는 policy를 의미한다.

예를 들어 미로 탈출 문제에서의 optimal policy는 다음과 같다.

Optimal policy란 expected utility(calculated reward)를 최대화 하는 policy이기에 reward의 설정에 따라 그 값이 달라진다는 것을 캐치하면 된다.

한편 눈여겨봐야 할 것은 -0.01과 -2.0이다.

-0.01의 경우 living panelty가 작아 굳이 위험을 무릅쓰고 탐색을 할 필요기 없으므로, 벽에 계속 머리를 박는다.

반대로 -2.0의 경우 living panelty가 너무 커서 탐색하는 것 자체가 위험하기 때문에, 그냥 최대한 빨리 죽어버린다.

그럼 이 policy는 어떻게 찾아야 할까?

그걸 설명하기 위해 우선 expected utility를 정의해보자.

MDP에서 expected utility란, agent가 어떤 state에서 행동을 시작해서, 최종적으로 가질 수 있는 reward의 추정값을 의미한다.

이 추정값을 찾기 위해 전 시간에 배웠던 expectimax를 사용한다.

예시를 보면서 이해해보자.

이 문제에서 Cool state의 expected utility는 얼마일까?

Cool state에서 depth 2 expectimax를 해보자.

원래대로라면 끝까지 탐색해야 한다! 다만 설명을 위해 나중에 배우게 될 Time-Limited Value의 개념을 끌어왔다.

대충 이렇게 탐색을 통해 구하는구나~ 정도만 알면 된다.

여하튼 위와 같이 풀 수 있고, 최종적으로 2라는 값을 얻는다.

Discounting

다시 한 번 정리하자면, utility는 어떤 action을 선택했을 때 계산되는 값 (곧바로 얻는 reward (living reward) + 한 단계 미래에 얻는 reward + 두 단계 미래에 얻는 reward…) 들 중 최댓값을 의미한다.

그런데 지금 내가 당장 얻는 reward와 미래에 얻는 reward의 가치가 같을까?

미래에 얻는 것은 어떻게 보면 추정이고, 내가 얻지 못할 가능성도 있는데?

이런 아이디어가 discounting이다.

Discounting은 미래에 얻는 reward의 가치를 떨어트리기 위해 $\gamma$로 weighting을 하는 것을 말한다.

예를 들어 $\gamma=0.5$이고, 순서대로 1,2,3을 얻는다고 하면 utility는 $1\cdot 1+0.5 \cdot 2+0.25 \cdot 3$이 된다.

Quiz

한번 퀴즈를 풀어보자.

1번의 답은 어떻게 될까?

b, c, d에 대해서 좌측, 우측으로 갈 때의 utility를 구해보자.

그러면 좌측으로 움직일 땐 전부 10, 우측으로 움직일 땐 전부 1이 나오므로 전부 좌측으로 간다.

2번의 답은 어떻게 될까?

b의 경우 좌측으로 움직이면 $0.1\times 10=1$, 우측으로 움직이면 $(0.1)^{3}\times 1=0.001$이므로 좌측으로 간다.

c의 경우 좌측으로 움직이면 $0.1^{2}\times 10=0.1$, 우측으로 움직이면 $0.1^2\times 1=0.01$이므로 좌측으로 간다.

d의 경우 좌측으로 움직이면 $0.1^{3}\times 10=0.01$, 우측으로 움직이면 $0.1\times 1=0.1$이므로 우측으로 간다.

3번의 답은 어떻게 될까?

좌측으로 움직일 때의 utility는 $\gamma^{3}\times 10$, 우측으로 움직일 때의 utility는 $\gamma \times 1$ 이므로,

$\gamma = \gamma^{3}\times 10$, $\gamma = 1/\sqrt{10}$이다.

3. Solving MDPs

이제 utility를 어떻게 구하는지 알았으니, 이로부터 optimal policy를 찾아내는 방법을 배울 차례이다.

Optimal Quantities

우선 optimal policy란 expected utility를 최대화하는 policy를 의미한다.

한편 optimal한 행동을 했을 때, state가 얻는 utility를 $V^{*}(s)$라고 하고,

q-state가 얻는 utility를 $Q^{*}(s,a)$라고 한다.

예를 들어 living reward가 없고, discount가 0.9일때 optimal policy는 화살표의 방향과 같다.

또한 $V^{*}(s)$는 표시된 숫자와 같다.

그리고 가능한 action이 동,서,남,북 4개이므로 각 state당 4개의 q-state가 있고, 각각에 대한 $Q^{*}(s,a)$는 위와 같다.

The Bellman Equation

Optimal한 policy를 찾는 방법은 위와 같다.

굉장히 단순하지만, 이 포스트의 핵심을 꿰뚫고 있다.

자 그럼, 어떻게 keep being optimal 할 수 있을까?

간단하다. Expectimax를 하면 된다.

Expectimax에 따라, state는 action 중 가장 좋은 결과를 가져오는 action을 고른다.

따라서 $V$는 가능한 q-value 중 최댓값이 된다.

이때 q-value는 expecimax에서 change node와 다를 바 없이 기댓값(확률 * 값)을 의미한다.

다만 그 값이 즉각 받는 reward + dicounting을 적용한 미래에 받을 reward 인 것만 주의해서 기억해두면 된다.

간단한 식이지만, 정말정말 중요하다. 아래의 모든 내용은 그냥 이 식을 응용하는 방법을 배우는 것에 불과하다.

Time-Limited Values

자 그럼 식은 알았고, 어떻게 optimal value를 구할까?

가장 확실한 방법은 끝까지 탐색해서 구하는 것이다.

그러나 이건 당연히 현실적으로 불가능하다.

시간이 부족할 뿐더러, 애초에 끝이 있는지조차 불명확하다.

그래서 나온 아이디어가 TIme-Limited Value다.

정해진 시간, 곧 정해진 깊이만큼만 탐색해서 optimal value를 구한다는 것이다.

Value Iteration

위 아이디어로부터 자연스럽게 반복적으로 $V_{k}$를 구하는 알고리즘이 등장한다.

별 거 없다. $V_0$ 부터 시작해서 차근차근 올라가며 $V_k$를 구하는 알고리즘이다.

왜 이렇게 되는지 보이는가?

간단히 해설해보겠다.

$V_0$는 당연히 0이 된다. Depth 0 만큼 탐색했으니.

Cool의 $V_1$은

$Q_1(cool, slow)=1$

$Q_2(cool, fast)=0.5\cdot 2 + 0.5\cdot 2=2$

이므로 fast를 선택해서 2가 된다.

또한, Cool의 $V_2$는

$Q_2(cool, slow)=1+\gamma \cdot 2=3$,

$Q_2(cool, fast)=0.5(2 + \gamma \cdot 2) + 0.5(2 + \gamma \cdot 1)=3.5$

이므로 fast를 선택해서 3.5가 된다.

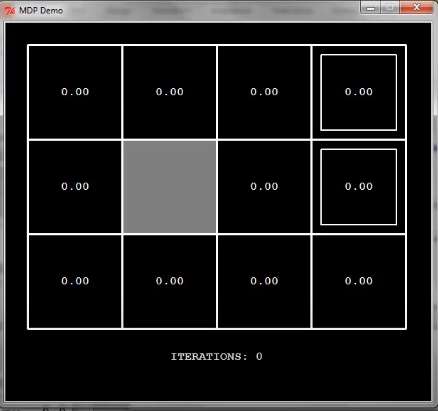
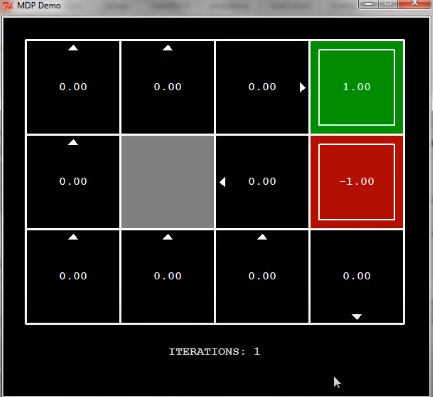
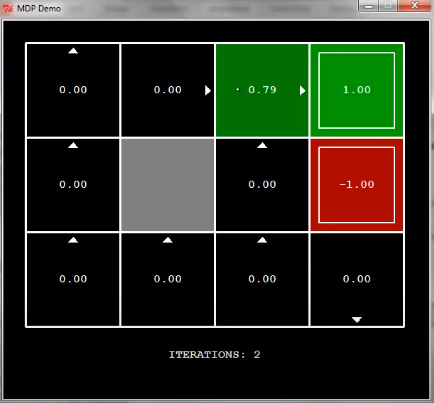
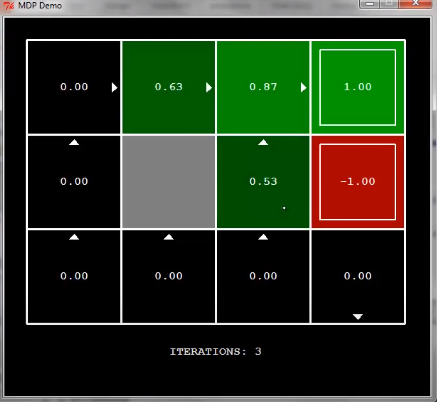
아래는 Demo를 캡쳐한 내용이다.

이걸 보고 이해 한다면 value iteration을 모두 이해한 것이다.

Convergence

Value Iteration을 제대로 이해했다면 한가지 의문이 들어야 한다.

수렴해야 optimal 할텐데.. 이게 결국 수렴하긴 하나?

다행히도, 두 가지 경우에 대해서는 수렴함이 증명되어있다.

첫 번째 경우는 너무 당연하고, 너무 극단적인 케이스다.

두 번째가 좀 더 일반적이지만, 증명이 살짝 어렵다.

직관적으로는 뭐.. 등비수열이니까 어느 한 값으로 수렴하겠지 라고 하겠지만, 증명은 항상 골때린다.

증명의 핵심은 $V_k(s)$가 한 레이어가 더 있다고 생각하는 것이다.

그러면 $V_k(s)$와 $V_{k+1}(s)$의 차이를 구할 수 있고, 이게 discounting 되므로 $k$가 계속 커지다보면 이 차이가 결국 사라지고, 수렴하게 된다는 것이다.

Policy Evaluation

Bellman equation을 활용하는 또 다른 방법은 policy evaluation이다.

Evaluation이라는 단어에서 짐작할 수 있듯이, 특정 policy에 대한 평가를 하는 방법이다.

이전에 배웠던 value iteration은 policy 없이 모든 action에 대해 계산을 하지만, policy evaluation은 이미 주어진 policy에 따를 때의 value를 계산해내는 것이다.

Policy가 이미 주어졌다는 말은 한 방향만 고려한다는 의미이므로, max를 취할 필요가 없어진다.

예를 들어, 두 policy에 대해 evaluation을 진행하면 이렇게 나온다.

복잡도는 어떻게 될까?

$S$를 state의 개수라 하면, 모든 state에서 $S$번 Q value를 계산하므로 $O(S^2)$이 된다.

Policy Extraction

한편으론, Value iteration을 통해 열심히 $V$를 가지고 optimal policy를 뽑아내야 할지 의문이 들 것이다.

간단하다. 그냥 최댓값을 만들어내는 action a를 고르면 된다.

이것이 policy extraction이다.

예를 들어 이 상황에서 Policy Extraction을 수행하면 빨간 동그라미가 쳐진 action을 policy로 선택하게 될 것이다.

식은 간단하다.

여기서 중요한 점은 action을 뽑아낼 때에는 q-value가 필요하다는 점이다.

이게 이후에 배울 강화학습의 핵심적인 원리가 된다.

Policy Iteration

이제껏 잘 써왔지만 Value Iteration은 사실 문제가 많다.

일단 너무 느리고, value보다 policy가 훨씬 먼저 수렴한다는 점을 이용하지 못한다.

이 예시가 이를 상당히 잘 보여준다. $k=5$일 때 이미 policy가 결정되었다는 사실이 놀랍지 않은가?

그럼 이 단점을 어떻게 보완해야 할까?

아이디어는 간단하다. Value iteraion을 policy level로 끌어내리는 것이다.

위 두 과정을 계속 반복하다보면 결국 optimal policy로 수렴하게 된다.

그런데 Improvement 과정이 살짝 이해가 안 갈 수도 있다.

Improvement를 다르게 말하자면 가장 높은 value를 가진 다음 state로 가는 action을 선택하는 것이다.

흔히 greedy improvement라고 부르기도 한다.

예를 들어 이렇게 evaluation을 진행한 다음 improvment를 수행하면

이와 같이 max state를 가리키도록 policy가 변화한다.

실제로 이렇게 무조건 높은 곳으로 가도록 바뀌지는 않는다. 수식에서 보이다시피 $R$과 $\gamma$를 복합적으로 고려해주어야 하기 때문이다. 대충 이런 느낌으로 improvement를 한다고 생각하면 된다.

4. Summary

iteration, extraction, evaluation.. 뭔가 많아보이지만 결국 전부 bellman equation을 응용한 것에 불과하다.

Bellman equation이 의미하는 바가 뭔지를 정확히 이해한다면, 이 내용들을 굉장히 쉽게 받아들일 수 있을 것이다.

RL에 관한 페이지들은 별 의미가 없어서 적지 않았다.