[AI] Search (2)

이 글은 포스텍 이근배 교수님의 CSED442 인공지능 수업의 강의 내용과 자료를 기반으로 하고 있습니다.

CSED442 인공지능 수업 2주차 두번째 강의 내용 요약이다.

Graph Search 부분이 ppt와는 다른 순서로 배치되어있다.

1. Informed Search 란?

지난 포스트에서 다뤘던 Uninformed Search 와 반대되는 개념이다.

정보를 이용하는, 구체적으로는 goal 에 가까운 방향인지를 알 수 있는 정보를 이용하는 Searching 이다.

2. Heuristic 이란?

A function that estimates how close a state is to a goal

핵심은 추정값이라는 것이다.

이 말은 같은 World 라도 문제나 상황에 따라 자유롭게 설정 할 수 있다는 얘기이다.

위 팩맨 게임을 예로 들어보자.

현재 팩맨의 위치에서 goal (좌측 하단 흰색 점) 까지의 거리는 어떻게 될까?

아마 초록색 경로의 길이가 될 것이다.

그럼 대강의 추정값은 어떻게 될까?

여러 방법이 있겠지만, 가장 간단한 Euclidean Distance 를 구할 수 있다. (빨간색 선)

그렇다면 goal 까지의 Euclidean Distance 를 반환하는 함수가 Heuristic 이 된다.

직관적으로 Heuristic 이 정확할수록 좋은 Searching 을 할 것이다.

그렇다면 실제 거리보다 작게 추정됐다면 어떻게 될까?

반대로, 실제 거리보다 크게 추정됐다면 어떻게 될까?

미리 답을 말해주자면 실제 거리보다 작게 추정된 경우에만 A* tree search 가 Optimal 하다. 증명

3. Greedy Search 란?

Expand a node that you think is closest to a goal state

Heuristic value 가 가장 작은 노드부터 확장해나가는 전략이다.

• Complete? : Loop 에 빠질 가능성이 있어서 No

• Optimal? : No.

• Time? : 최악의 경우에는 $O(b^m)$. 다만, 좋은 heuristic 을 선택할수록 걸리는 시간을 크게 줄일 수 있다.

• Space? : 최악의 경우 모든 경로를 다 저장하므로 $O(b^m)$

4. A* Search 란?

Greedy Search + Uniform Cost Search

Greedy Search 의 heuristic $(h(n))$과 UCS 의 path cost $(g(n))$를 합친다.

수식으론 $f(n)=g(n)+h(n)$ 으로 표기한다.

간단히 과거와 미래 값을 모두 사용한다고 생각하면 된다.

당연히 tree search로 구현가능하겠지만, 특별히 하나 더 알아보자.

1. A* tree search

2. A* graph search

차이점은 하나다. A* graph search는 같은 노드를 두 번 방문하지 않는다.

A* graph search의 수도코드를 보면, 나머지는 tree search와 다 똑같고 이전에 방문했던 노드인지 확인하는 부분만 추가되었음을 알 수 있다.

1. When should A* terminate?

A* search를 이해할 때 주의할 점은 goal 이 fringe 에서 dequeue 할 때 탐색이 끝난다는 것이다.

직관적으로는 설령 enqueue 했더라도 fringe 에 그보다 적은 비용의 node 가 남아있다면 그 노드를 거쳐가는 경로가 optimal solution 일 가능성이 존재하기 때문이다.

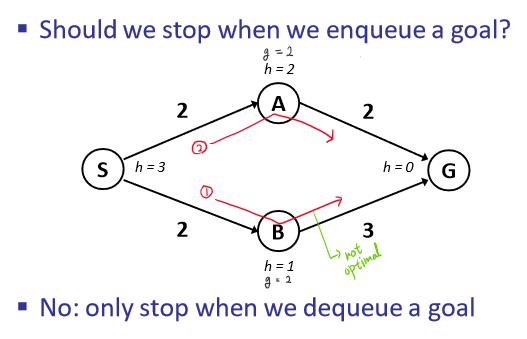
위 그림을 보면 이해가 갈 것이다.

정확한 이유는 증명을 보면 알 수 있는데, enqueue 할 때 끝난다고 가정해버리면 증명 자체가 성립이 안된다.

2. Optimality of A* Search

자 그럼, A* search는 optimal 할까?

재미있게도, A* tree search는 heuristic이 admissible 하면 optimal 하고

A* graph serach는 heuristic이 consistent 하면 optimal 하다.

그럼 admissible은 뭐고 consistent란 뭘까? 하나하나 알아보자.

Admissible 이란?

A heuristic h is admissible if $0\leq h(n)\leq h^{*}(n)$

$h^{*}(n)$ 은 실제 비용을 의미한다.

Admissible, 즉 인정가능한 heurisitic이란 실제 비용보다 작게 추정한(= 과대평가 하지 않아야) heurisitic을 의미한다.

Admissible 해야 optimal한 이유는 생각해보면 당연한데, optimal 한 경로가 실제 비용보다 높게 추정된다면 해당 경로를 선택하지 않을 수도 있기 때문이다.

엄밀한 증명

Consistent 란?

A heuristic h is consistent if $h(n)-h(n_{child})\leq cost(n\;to\;n_{child})$

모든 이동은 그 이동으로 인한 heuristic의 감소가 해당 이동의 실제 비용보다 작아야 한다는 얘기이다.

다른 말로 하자면, 모든 노드로부터 목표 지점까지의 추정 비용을 과대평가하지 않을 뿐만 아니라, 그래프 상에서 간선으로 이어진 모든 두 노드에 대해서도 똑같은 원칙으로 동작해야 한다는 얘기이다.

Consistent heurisitc의 가장 중요한 성질은 $f(n)$이 단조 증가한다는 것이다.

왜냐하면 노드 $n$와 그 자식 노드 $n_{child}$이 있을 때 consistency가 보장되면,

$f(n_{child})=g(n_{child})+h(n_{child})=cost(n\;to\;n_{child})+g(n)+h(n_{child})\geq g(n)+h(n)=f(n)$ 이기 때문이다.

어떻게 보면 당연한 소리이다.

갑자기 자식 노드에서 goal로 점프하지 않는 이상 이 일관성은 지켜지기 마련이기 때문이다.

또한 단조 증가한다는 말은 중간에 다른 경로로 새지 않고 계속해서 goal을 향해서 나아간다는 얘기이므로 optimal하다고 생각할 수 있다.

Optimality of A* tree search 증명

A* tree search의 optimality에 대한 엄밀한 증명은 다음과 같다.

• A 는 optimal goal node 이다.

• B 는 suboptimal goal node 이다.

• h 는 admissible 하다

Claim: A will exit fringe before B

Proof:

B 와 A 의 ancestor 노드 n 이 fringe에 있다고 하자.

1. $f(n)$ 은 당연히 $f(A)$ 보다 작다 ($f(A)=g(A)\geq g(n)\geq f(n)$)
2. $f(A)$ 는 $f(B)$ 보다 작다 (optimal 이므로)
3. 따라서 $f(n) < f(B)$ 이므로 n 이 먼저 확장된다

모든 n 이 B 보다 먼저 확장되면 최종적으로 A 가 B 보다 먼저 확장될 것이다.

$\therefore$ optimal

Optimality of A* graph search 증명

A* graph search의 optimality에 대한 엄밀한 증명은 다음과 같다.

• A 는 optimal goal node 이다.

• B 는 suboptimal goal node 이다.

• h 는 consistent 하다

Claim: Prove when $n$ is selected for expansion, an optimal path to $n$ has been found

Proof by contradiction:

A* graph search가 $n$을 확장시켰지만 $n$에 대한 optimal path가 찾아지지 않았다고 가정해보자

그러면 $n$에 대한 optmial path 위에 있는 $n’$은 fringe에 있을 것이다.

어떤 path에 대해서도 $f(node)$는 단조 증가하므로, $f(n)\geq f(n’)$

그렇다면 $n’$은 $n$보다 먼저 확장되어야 했으므로 모순이다.

$\therefore$ optimal

Evaluation of A* Search

• Complete? : Yes

• Optimal? : Yes (If tree search: admissible, graph search: consistent)

• Time? : 최악의 경우에는 $O(b^m)$. 다만, 좋은 heuristic 을 선택할수록 걸리는 시간을 크게 줄일 수 있다.

• Space? : 최악의 경우 모든 경로를 다 저장하므로 $O(b^m)$

사실 Greedy 나 A* 처럼 Heuristic 에 크게 의존하는 경우에는 complexity 가 그닥 의미가 없다고 생각한다.

그래서 ppt 에 없나?

3. UCS vs A*

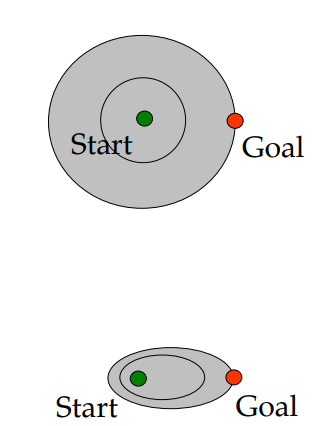
위쪽이 UCS 고 아래쪽이 A* Search 이다.

보다시피, UCS 는 모든 방향을 탐색하는 반면 A* Search 는 goal 방향 위주로 탐색한다.

훨씬 효율적이다!

4. Creating Admissible Heuristics

글을 쭉 읽었다면 한가지 의문이 들어야 한다.

어떻게 Admissible Heuristic 을 만들지?

간단하다. 제약을 줄인 relaxed problem 을 풀면 된다!

제약을 줄이면 그만큼 goal 에 도달하기 쉬워지고, 곧 admissible heuristic 을 만들 수 있다.

또한 heuristic 을 만드는 것 자체도 쉬워진다.

제일 좋은 예시는 8 Puzzle 이다.

8 Puzzle

8 Puzzle 이란 1,2,3,..,8 타일을 움직여 그림의 Goal State 처럼 만드는 것이다.

보다시피 다른 타일 때문에 타일을 움직이기 어려워 heuristic 을 구하기도 힘들다.

여기서 relaxed problem 을 도입하자.

1. Number of tiles misplaced

타일을 detatch-attatch 가 가능하다고 생각해보자.

그러면 Heuristic 은 단순히 잘못된 위치에 있는 타일의 개수가 된다.

이건 Admissible 할까? 당연히 그렇다.

2. Ignore other tiles

이번엔 타일을 다른 타일들을 무시하고 움직일 수 있다고 하자.

그러면 Heuristic 은 각 타일들이 움직여야 하는 거리의 합이 된다.

예를 들어

이 State 의 heuristic 은 무엇일까?

7 타일은 3번 움직여야 하고, 2 타일은 1번 움직여야 하고, 4 타일은 2번 움직여야 하고..

곧 다 합쳐서 $3+1+2+\cdots=18$ 이 된다.

1번 relaxed problem보단 더 정확한 (= 더 큰) heuristic 을 얻는데 성공했다.

확연하게 성능이 향상되었음을 볼 수 있다!

3. Acture cost

만약 아예 heuristic 을 실제 cost 로 정하면?

당연히 Best 다.

그러나 이 경우 heuristic 을 계산하는 연산 비용이 상당히 비싸진다.

이처럼 heuristic 에는 trade-off 가 존재한다.

quality of estimate 와 work per node 를 적절히 조절해서 heuristic 을 만들어야 한다!

6. Trivial Heuristics, Dominance

모든 Heuristic 값이 더 크면 Dominance 라고 말한다.

곧, 더 정확한 heuristic 이라는 것이다.

또한 두 개의 Admissible Heuristic 의 max 값도 당연히 admissible 하다.

그리고 bottom lattice 를 zero 라고 부르는데, 이건 Uniform-cost search 와 동일하다.

7. 출처 및 참고 자료

끝까지 간다 님 블로그