[AI] Search (1)

이 글은 포스텍 이근배 교수님의 CSED442 인공지능 수업의 강의 내용과 자료를 기반으로 하고 있습니다.

CSED442 인공지능 수업 2주차 강의 내용 요약이다.

1주차는 드랍 기간이라서 인공지능 소개 정도의 수업이었다.

1. Agent 란?

인공지능에서 Agent 란 독자적으로 행동하는 하나의 주체를 의미한다.

예를 들어, 롤에서 사용자 모드 봇 각각이 agent 라 할 수 있다.

Agent 의 핵심은 행동한다는 것이다.

이 행동이 어떤 전략을 기반으로 하는가에 따라 agent 의 종류가 나뉜다.

찾아보니까 굉장히 많은 종류가 있는데, 수업에선 심플하게 두 종류만 소개했다.

1. Reflex agents

결과를 고려하지 않고 현재 인식만을 기반으로 결정한다

단순하다. 결과는 모르겠고, 일단 하고 본다는 것이다.

위 그림이 참 직관적으로 잘 표현하고 있다.

사진의 Reflex Agent 는 사과를 보면 따야한다는 전략을 가지고 있다.

그래서 그냥 뛰어들고 본다.

뛰어들면 절벽으로 떨어지지만, 그런건 신경쓰지 않는다.

구현을 위해서는 현재 상태에 대한 기억 또는 model이 필요하다.

2. Planning Agents

행동에 따른 결과 또한 고려하여 결정한다.

Reflex agent 보다 한층 지능이 성장했다.

내가 이걸 하면 어떻게 될까? 를 질의해보고 결정한다.

위 그림의 agents 는 무작정 뛰어들지 않는다.

아마도 그냥 뛰어들면 떨어진다는 것을 깨닫고 다른 방법을 시도하는 중일 것이다.

구현을 위해서는 우선 행동에 따라 상황이 어떻게 변하는지를 시뮬레이션 할 수 있는 model이 필요하다.

그리고 목표 (goal) 이 있어야 한다.

Optimal vs Complete planning

optimal 이란 최적, 최소의 비용의 해를 찾는 것이다.

complete 란 그냥 해만 찾는다. 최적인지 아닌지는 신경쓰지 않는다.

Planning vs Replanning

planning 은 한 번에 모든 경우의 수를 검토하여 행동하는 걸 말한다.

첫 행동 개시까지 상당한 시간이 소요된다.

replanning 은 제한된 depth 까지만 검토하고 행동하는 걸 말한다.

상대적으로 planning 보다 첫 행동이 빠르다.

2. Search Problem 이란?

Agent 는 어떤 선택이 좋은 결과로 이끄는지 탐색(Search) 해야한다.

곧, 이 문제를 Search Problem 이라 부른다.

1. Search Problem 의 구성요소

Search Problem 은 아래의 요소들로 구성된다.

1. A State space : models how the world is

2. A Successor function (with actions, costs) : models how it evolves in response to your action

3. A start state and a goal test

기본적으로 World 를 추상화(= model)한다고 생각하면 된다.

예시를 통해 구체적으로 알아보자.

State 란 두 상황이 다르다고 판단할 수 있는 기준이다.

위 팩맨 게임의 World State 는 무엇일까?

• 팩맨 위치 (120)
• 먹이 수 (30)
• 유령 위치 (12)
• 팩맨 방향 (NSEW)

등이 있다.

이 중에서 필요한 State 만 골라서 (추상화) 가능한 모든 상황을 모아둔 것이 state space 이다.

이런 space에서 (action, cost) 에 따라 상황이 어떻게 변하는지에 관한 함수가 successor function 이다.

그리고 그 함수의 시작과 끝이 a start state and a goal test 다.

이 세 가지는 같은 world 라도 문제에 따라서 달라진다.

두 가지 예를 들어보겠다.

1. Pathing Problem(단순히 팩맨의 위치만 중요한 문제)

• state space: 팩맨의 위치만 고려하므로 총 120 개

• successor function: 팩맨의 이동에 따라 팩맨의 위치 값을 변경시킬 것

• goal test: 특정한 지점에 도달하는 것

2. Eat-All-Dots(어떤 먹이를 먹은 것 까지도 고려해야 하는 문제)

• state space: 위치와 먹이의 상태를 고려하므로 $120\times2^{30}$ 개

• successor function: 팩맨의 이동에 따라 팩맨의 위치 및 먹이의 on/off 값을 변경시킬 것

• goal test: 모든 먹이를 다 먹는 것

2. State Space Graphs

A mathematical respresentation of a search problem

state space 를 graph 로 그린 것이다.

곧, 각 노드(world configuration)의 중복이 발생하지 않는다.

다만 그 많은 노드들을 한 번에 표시할 수 없어서 전체 그래프를 메모리에 구축하기는 어렵다.

근데 유용하게 쓰인다고는 한다.

3. Search Tress

A “what if” tree of plans and their outcomes

planning 을 tree 구조로 표현한 것이다.

start state 를 root node 로 놓고, plan에 따라 어떻게 state 가 변하는지를 보여준다.

마찬가지로 전체 트리를 다 한 번에 메모리에 올릴 수는 없다!

중복이 발생하기 때문에 무한히 트리를 확장할 수 있기 때문이다.

Searching with a Search Tree

3번부터는 이 Seach Tree 를 가지고 하는 searching 에 관해서 논한다.

알고리즘은 아래와 같다.

fringe 란 현재 선택 가능한 노드의 collection 을 말한다.

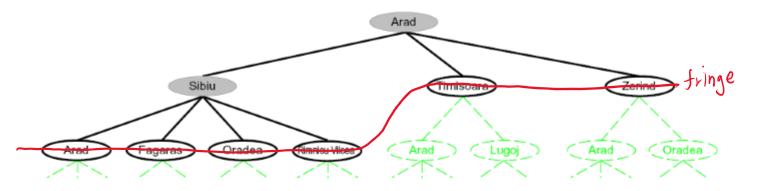
위 tree 에서 Arad 와 Sibiu 를 확장했다면, 빨간색 선을 지나는 노드들이 fringe 에 들어가 있다.

핵심은 fringe 에서 strategy 에 따라 노드를 선택하고, 확장한다는 것이다.

어떤 fringe 를 선택하느냐 (stack? queue?) 혹은

어떤 strategy 를 선택하느냐 에 따라 다른 searching 이 된다.

이 Searching 을 분석하는 4가지 지표는 다음과 같다.

• Completenss : 해를 찾을 수 있는가?
• Optimality : 최적해를 찾을 수 있는가?
• Time : 해를 찾는데 걸리는 시간
• Space : 검색에 필요한 메모리 공간

3. Uninformed Search Methods

Uninformed Search 란 말 그대로 정보가 없는 상태에서의 searching 이다.

여기서 말하는 정보란 시작 부분부터 목표까지 도달하는데 얼마나 많은 단계가 존재하는지, 목표까지 가는데 얼마나 걸리는지 등 사전에 주어지는 정보를 말한다.

주의 : 그림에 맞추다 보니 tier 를 표시하는 기호가 m, s, d 등 중구난방이다. 모두 같은 의미이다!

1. Depth First Search

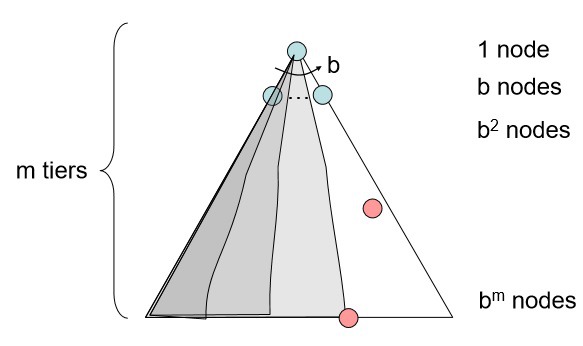
Expand a deepest node first

깊이를 우선으로 탐색하는 전략이다.

흔히 fringe 를 LIFO stack 으로 만들어 구현한다.

• Complete? : 깊이가 무한정 길거나 순환이 있어서 갇히지 않는 경우에만 complete 하다.

• Optimal? : left most 해를 찾으므로 Optimal 이라고 볼 수 없다.

• Time? : 전체 트리를 탐색할 수도 있으므로 $1+b+b^2+\cdots+b^m=O(b^m)$

• Space? : 탐색중인 tier 에서는 b 개의 경로가, 그 이전의 각 tier 에서는 b-1 개의 대체 경로가 있으므로 $b+(b-1)+(b-1)+\cdots+(b-1)=O(bm)$ 이다.

2. Breadth First Search

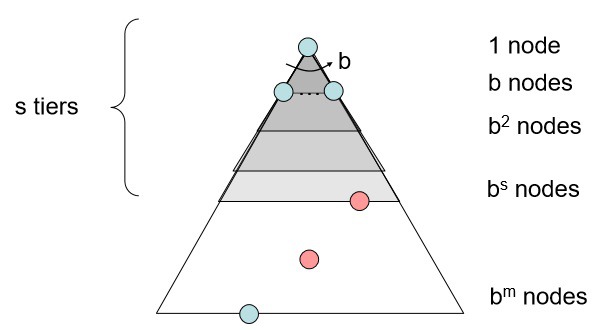
Expand a shallowest node first

너비를 우선으로 탐색하는 전략이다.

흔히 fringe 를 FIFO queue 로 만들어 구현한다.

• Complete? : 유한하다면 언젠가는 해에 도달할 수 있으므로 complete 하다.

• Optimal? : 모든 경로의 cost 가 동일하다면 (= unweighted 라면) Optimal 하다.

• Time? : 전체 트리를 탐색할 수도 있으므로 $1+b+b^2+\cdots+b^s=O(b^s)$

• Space? : 대강 last tier 가 fringe 에 있으므로 $O(b^s)$

3. Iterative Deepening

DFS 와 BFS 의 이점을 적절히 취해 합친 형태이다.

탐색 깊이 한계를 정해서 DFS 를 돌린다.

ex)

Run a DFS with depth limit 1. If no solution…

Run a DFS with depth limit 2. If no solution…

Run a DFS with depth limit 3. If no solution…

• Complete? : Yes

• Optimal? : BFS 와 같다.

• Time? : BFS 와 같다. $O(b^d)$

• Space? : DFS 와 같다. $O(bd)$

언뜻 보면 했던 경로 또 탐색(DFS)하니까 비효율적이지 않나 싶어 보인다.

그런데 대체로 low level 에서 끝나서 그렇게 비효율적이진 않다고 한다.

4. Uniform Cost Search

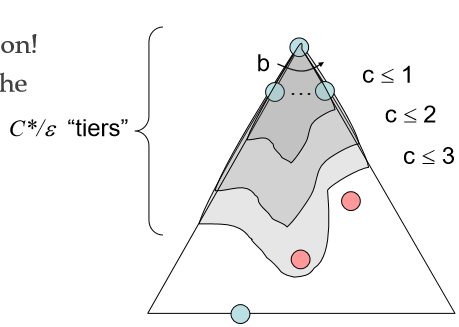
Expand a cheapest node first

낮은 비용의 경로를 우선으로 탐색하는 전략이다.

이때 누적된 비용을 기준으로 함에 주의하자!

흔히 fringe 를 priority queue 로 만들어 구현한다.

• Complete? : Cost 가 양수 값을 가진다면 complete 하다.

• Optimal? : Optimal 하다.

• Time? : $O(b^{C^{*}/e})$

• Space? : $O(b^{C^{*}/e})$

왜 Optimal 인지에 대한 증명은 다음 포스트의 A* 증명과 방법이 동일하다.

Time/Space complexity 의 증명

$C^{*}$ 는 goal 까지의 cost.

$\epsilon$ 은 최소 소모 비용.

Tree 의 최대 깊이는 $C^*/\epsilon$ 이 된다.

한편 UCS 에서 최악의 경우는 모든 경로의 cost 가 같아서 BFS 처럼 동작해야만 하는 경우이다.

따라서 Time/Space complexity 는 $O(b^{C^{*}/\epsilon})$ 가 된다.

그런데 찾아보면 다른 책에서는 $O(b^{1+C^{*}/\epsilon})$ 로 소개하고 있다.

정확히 무슨 차이인지는 모르겠지만, 아마 첫 노드 탐색을 고려하냐 마냐의 차이인 것 같다.

수업에서 가르쳐준대로 하자 ㅎㅎ..

단점

USC 의 단점은 무엇일까?

바로 goal 에 대한 아무 정보가 없기 때문에 탐색이 효율적이지 못하다는 것이다.

이것을 보완한 것이 다음 포스트의 Informed Search 이다.

5. The One Queue

이론적으로 위의 전략들은 모두 priority queue 로 구현이 가능하다.

다만 보통 DFS 나 BFS 는 $log(n)$ 의 overhead 를 막기 위해 스택이나 큐로 구현한다.

6. 요약

위 전략들을 요약한 표이다.

4. 출처 및 참고 자료

1ambda 님 블로그

pizzaplanet 님 블로그

복습은만점의지름길 님 블로그